[Rescued from my old blog.]
Marjorie in AZ asked a terrific question on the (now defunct) AHFH Math forum:
“…I have always been taught that the order of operations (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction) means that you work a problem in that order. All parenthesis first, then all exponents, then all multiplication from left to right, then all division from left to right, etc. …”
Many people are confused with order of operations, and it is often poorly taught. I’m afraid that Marjorie has fallen victim to a poor teacher — or at least, to a teacher who didn’t fully understand math. Rather than thinking of a strict “PEMDAS” progression, think of a series of stair steps, with the inverse operations being on the same level.
Parentheses
First do whatever is inside parentheses or brackets, from the innermost set outward. Parentheses are used when necessary to override the ordinary order of operations, to communicate that certain things within your equation belong together. Within each set of parentheses or brackets, follow the normal order of operations. Be aware that some other mathematical symbols, such as the radical sign and the fraction bar, double as an understood set of parentheses. That is, if you have a complicated algebra fraction, you need to treat it as if there were brackets around the entire numerator and around the entire denominator.
Exponents and Roots
These are inverse operations, which means they are just two different ways of looking at the same mathematical concept. They are the highest level in the normal order of operations, indicating repeated multiplication. Exponents and roots all need to be calculated before any multiplication, addition, etc., unless there are parentheses that dictate otherwise. On any single level of operation (such as this exponents-and-roots level), work from left to right through your equation.
Multiplication and Division
These are inverse operations, which means they are virtually interchangeable. Division could be written as multiplication: think of the rule for dividing fractions. This is the middle level in the normal order of operations, indicating repeated addition. Multiplications and divisions all need to be done before any addition or subtraction, unless there are parentheses that dictate otherwise. On any single level of operation (such as this multiplication-and-division level), work from left to right through your equation.
[Hint: In a complex equation, it is a good idea to change all the divisions into multiplying-by-the-reciprocal before doing any calculation.]
Addition and Subtraction
These are inverse operations, too. They are the lowest level in the normal order of operations, and they all need to be done last, unless there are parentheses that dictate otherwise. On any single level of operation, work from left to right through your equation.
[Hint: In a complex equation, it is a good idea to change all subtractions into adding-the-opposite before doing any calculation.]
Notice that we do the repeated operations first. Powers are repeated multiplication, and multiplication is repeated addition. We could, if we felt masochistic, try to convert the powers into multiplications, and then convert the multiplications into additions — and then we wouldn’t have to worry about what order to do everything in. Addition is both associative and commutative, which means it can be done in any order. But I don’t even want to think about what a mess an equation like that would be, especially with algebra variables. Yuck! Much better to learn and follow the standard order.
Students often feel that order of operations is an arbitrary rule, like driving on the right (or left, depending on where you live) side of the road. Like driving on the proper side of the road, however, such arbitrariness does NOT mean that the rule is unimportant. If you think of it as I’ve described here, you may save yourself and your students a few mathematical wrecks!
(21 + 3) / 6(2)
Correct me if I’m wrong….I would divide 24 by 12. If the back slash had been an actual division sign, I would still have dealt with “all paranthesis” first. What’s your take??
Typed that way, like in an email, it is ambiguous.


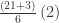
I would interpret it as you did, this way:
But if the person who typed it meant:
which would be the same as:
then it should be worked from left to right, first dividing 24 by 6 and then multiplying by 2.
Whoever typed the calculation should have added a set of brackets to make his intention clear. This sort of thing is why I tend to overuse parentheses and brackets when typing math in emails. I like to avoid ambiguity whenever possible.
could you help me solve this
8÷2-4×3+4=z
it is writtend exactly as this.
would be grateful if you could also mail the solution to me too.
thanks a lot
Karan
Karan, did you read the article above? Just follow the normal Order of Operations: Do the division and multiplication first. Write down the new equation that gives you. Then do the subtraction and addition, in order, from left to right.
I NEED PROBLAMS!!!
How would this be solved???
2-((7-6) + (9-19))
Can you explain what to do with the – and + signs outside of the ( )’s. Thanks!
Hi, Jackie!
You need to work parentheses from the inside out, so find the parentheses that are “farthest in” and do those first. In your problem, you can start with either the (7-6) or the (9-19). Whichever one you choose, do that calculation and then copy your problem on the next line of your page, with the answer in place of the parentheses:
2 – ( (7 – 6) + (9-19) )
= 2 – (1 + (9 – 19) )
Then work the next set of inner parentheses. Each time you do part of the calculation, rewrite your problem with that answer in the place where the parentheses had been. That leaves you ready for the next step
= 2 – (1 + -10)
etc.
I don’t get this problem.
20+100÷5
_______ +7=
40÷8
Can anyone help me?
Is that meant to be a fraction? If so, then you need to treat the top of the fraction (numerator) and the bottom (denominator) as if they both have parentheses around them. The bar in a fraction acts like parentheses, too, so simplify the top and bottom of your fraction and then continue with the rest of the equation.
Please solve my maths problem given below step by step.
x (1+5/200) * (10/100)
where x is the value.
i want to know by which factor x has to be multiplied.
Chary, I don’t think you have copied the problem correctly, but in the expression you gave, x is multiplied by both factors. Each of the parentheses is a factor multiplying x.
This is not a Help Forum. If you need to ask questions about your homework, there are many places online that are set up for that sort of thing. Check my Free Math Resource Page.
I will not answer any more homework questions on this page.
Do not post them.
I will delete them.
You can have an amazing site with online math games for free!
Here Order of Operations Games from the site: Order of Operations Games
and to the main site: Math Games
If parenthesis are place around the entire problem, ie. (9 – 4 + 52 + 1 x 44) would you just work from left to right or solve the x first then work left to right with the subtraction and addiiton?
Within any set of parentheses, you still follow the order of operations. So if you have parentheses within the parentheses, be sure to do the innermost set of parentheses first. If you have mixed operations within the parentheses, multiplication and division still always comes before addition and subtraction.
The only time that the left-to-right rule applies is for operations at the same level. So for instance, if you have several multiplication and division things to do, because those are all on the same level, you will work them from left to right.
Another thing to consider, however, is that multiplication is associative and commutative. If all you have is multiplication (not division!), then you can move them around and work them in whatever order makes the calculation easiest.