Alex handed her brother Leonhard a box wrapped in the rocket tessellation paper, with air holes carefully punched in two sides.
“Merry Christmas, Leon!” she said.
He ripped open the gift. Alex winced. Boys have no artistic appreciation, she thought.
“Oh, cool! Thanks,” Leon said.
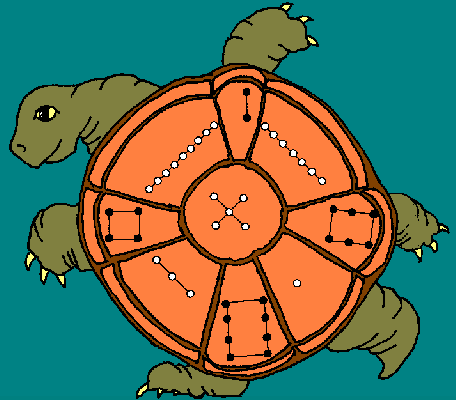
“His name is Lo-shu,” said Alex. “But be careful. I used non-toxic tempera paint. The design will was off.”
Leon turned the turtle and studied the back of its shell. “Oh, that’s just like in the legend! I’ll copy it down before I let him near any water.”
- What do the shapes on Lo-shu’s back mean?
- Why are some dots white and some black?
Magic Multigrades
Leon spent the afternoon at his desk. He was so quiet that Alex stuck her head in the door.
“You must be up to something,” she said.
“Hey, look.” He held up his copy of Lo-shu’s magic square. “If I take the numbers in the top and bottom rows:
Alex laughed. “Of course, silly. That’s what a magic square does.”
“Yes, but how about this:
Alex leaned over his shoulder. “Wow! I never noticed that. What about the middle row? … No, it’s different.”
“I was trying to find another set of numbers that worked that way,” Leon said. “Want to help?”
Sets like {2, 4, 9} and {1, 6, 8}, where the sums of the numbers are equal and so are the sums of the squares, are called multigrades. Alex and Leon found one other pair of multigrades in the 3×3 magic square.
- Can you find the other magic square multigrades?
Leon Challenges Alex
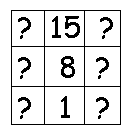“Here, Alex,” Leon said. “I made up a new magic square. Do you think you can finish it?”
Alex took the piece of paper and frowned. “No way! I bet there’s almost a zillion ways to fill this in.”
“Here’s a hint: I gave the max and min.”
“No negative numbers, at least,” Alex said. “Okay, let me see…”
She studied the paper for several minutes. “Nope. Even limited to the numbers between 1 and 15, I see at least three ways to do it.”
“Yes,” Leon said, “but mine is the perfect solution.”
- With that clue, Alex was able to finish the magic square. How did she do it?
Edited to Add
Answers to this and other Alexandria Jones puzzles are now posted:
To Be Continued…
Read all the posts from the November/December 1998 issue of my Mathematical Adventures of Alexandria Jones newsletter.
Denise Gaskins' Let's Play Math 
it can be learn more in math it have intruction