Homeschool Musings: Math Manipulatives Part 3

We’ve talked about several types of math manipulative that homeschooling parents might use to help their children learn math (see part 1 and part 2), but we never stopped to ask the most basic question:

Why use math manipulatives at all?

Math manipulatives are a tool for solving educational problems, so we should first decide what problem we are trying to solve. That will help us know which tool to use.

What do we want math manipulatives to do?

Do we want a tool that will help our children:

• Practice counting, matching each number with the appropriate quantity of objects?
• Model basic arithmetic facts?
• Visualize place value to understand how the standard algorithms work?
• Explore number relationships in creative ways to build fluency?
• Play with the big ideas of math, the fundamental concepts that form the foundation of arithmetic and algebra?

If the first two points describe your goal, found objects will work fine. There’s no reason for you to waste money buying math blocks.

For those who are working toward mastery of the standard pencil-and-paper methods (algorithms) for calculation, that’s exactly what base ten blocks are designed for.

If you want to play with number relationships, build number sense, and develop fluency in arithmetic, the scaled Mortensen or Math-U-See block will serve you well.

But if you’re like me, if what you really want is for children to grapple with the big ideas of math, to play hands-on with the fundamental nature of numbers, to discover how things work and why the rules are true — if that’s your goal, then you need to consider a different sort of math manipulative.

The big ideas of number relationships are found in algebra, not in arithmetic. If we want to bring our children into direct contact with these ideas, we need to teach with algebra in mind from the very beginning.

Scaled rods without markings

Cuisenaire rods are ten plastic or wooden blocks ranging from one to ten centimeters long, with each length painted a distinct color but with no markings to distinguish their size.

These rods are designed to avoid counting, to turn children’s minds away from thinking about quantity so they can focus on relationships. The rods do not have to represent counting numbers, or even rational numbers: They can represent any length at all, so children are working with real numbers from the very beginning.

With Cuisenaire rods, we can teach algebra before arithmetic, bringing children into direct contact with the very structure of mathematical relationships and laying a strong foundation of understanding without being distracted by the details of calculation.

Using the color names as variables, young children can play with the concepts of addition, subtraction, multiplication, fractions, squares and square roots, higher powers and roots, exponents, logarithms, arithmetic and geometric series and more.

At each stage, students go far beyond surface-level vocabulary. They master the underlying structure of algebraic relationships, learning to create and manipulate their own math equations.

Algebra before arithmetic

For example, we might investigate this block pattern:

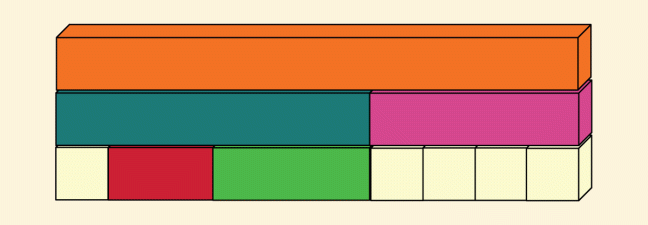
Orange
= dark green + purple
= (white + red + light green) + (4 whites)

…which can be written with letters as:
o = d + p
= (1/6 × d + 1/3 × d + 1/2 × d) + (4 × 1/4 × p)

This equation is true for ALL numbers. The orange rod can represent any number you want to choose. That number can also be viewed as the sum of two smaller numbers, shown here as the dark green and purple rods. And those two smaller numbers may in turn be broken into even smaller parts, which are themselves related together by addition, multiplication, or other math operations.

The rods are limited by their physicality, but a child whose mind has been awakened to these relationships can build on this knowledge to fill a whole page with creative mathematical expressions.

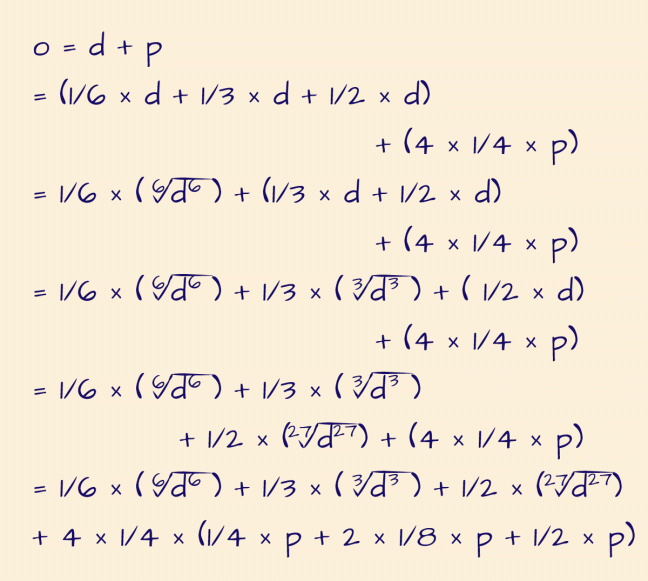
And ever on, as the expression grows in delightful complexity, each line representing the child’s conception of an algebraic relationship and the whole composition a playful exploration of that high and mountainous land of mathematics.

From algebra to arithmetic

When we are ready to add number calculations into our mathematical play, children easily apply their algebraic mastery to manipulating arithmetic calculations.

For example, if we begin with the basic rod pattern from earlier and let the orange rod represent 500, a child might write:

And so on, combining number relationships in playful, creative ways that express both understanding and joy.

Find out more about how this works in next week’s post…

• Math Musings: Teaching the Big Ideas

How can we teach this way?

The main difficulty in teaching algebra before arithmetic is that it’s so very different from the way we adults learned math. It requires parents and teachers to make a major shift in the way we think.

To change our minds is hard, but we will be rewarded with new understanding of our own as we learn along with our children.

This way of teaching algebra before arithmetic was pioneered by Caleb Gattegno. You can find his books at the Educational Solutions website. You may also find Madeleine Goutard’s book Mathematics and Children useful, as it builds on Gattegno’s work and gives tips for teaching math.

My friend Sonya Post has spent years mastering the algebra-first basics of Gattegno math, adapting it to work in a homeschool setting, and coaching other parents how to make the transition to this revolutionary, thought-provoking, concept-rich way of teaching math.

Now she’s put her method into an online course with step-by-step video instructions, open-ended printable homework, and weekly live workshops both for parents and students.

Oh, I wish this had been available back when my children were young!

You can read all the details here:

Learning Well at Home Courses ❯
(Use my affiliate code LPMBLC15 at checkout to save 15%.)

Everyone starts at the beginning and proceeds at their own pace. With older children, you’ll want the 2-course bundle because they’ll go through the lessons faster. But since even the first parts of the course are about algebraic thinking, no students are “behind” their age peers.