Puzzle: Patty Paper Trisection

One of the great unsolved problems of antiquity was to trisect any angle, to cut it into thirds with only the basic tools of Euclidean geometry: an unmarked straight-edge and a compass.

Like the alchemist’s dream of turning lead into gold, this proved to be an impossible task. If you want to trisect an angle, you have to “cheat.” A straight-edge and compass can’t do it. You have to use some sort of crutch, just as an alchemist would have to use a particle accelerator.

One “cheat” that works is to fold your paper.

I will show you how it works, and your job is to show why.

Gather Your Materials

• A piece of paper with square corners. (I used patty paper.)
• A ruler or other straight-edge.
• A pen or pencil.

One Step at a Time: The Red Lines

Draw any random angle (less than 90 degrees) with its baseline along the bottom of your paper and its vertex at the corner. This angle is black on the image below.

Call the vertex point P.

Fold your paper horizontally, so that point P touches the side of the paper at some other point Q. Press down this fold to make the lower red line in the image.

Without unfolding your paper, draw a line through Q, using the baseline edge as your guide (the upper red line in the image).

Then unfold the paper, and trace the line of the fold.

• Can you prove that these two lines are parallel to the baseline of your paper?
• Can you show that they must be equally spaced?

The Blue and Green Lines

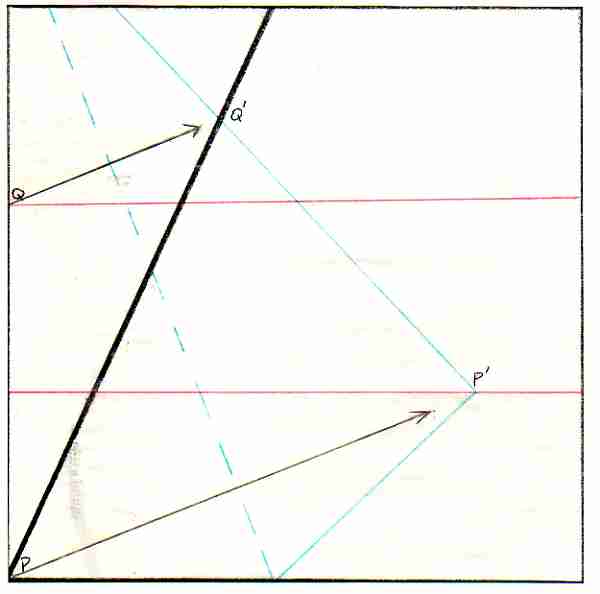
Now fold the paper at a slant so that point P touches the lower of the two parallel lines. This fold creates the dashed blue line in the image. Draw along the edge of the paper to make the solid blue line.

Notice that point Q touches the top line of your original angle. These touchpoints are labeled P’ and Q’ on the diagram above. Mark them on your paper.

Unfold the paper.

Use your straight-edge to connect corner P with point P’. Also draw a line from corner P through the point where this blue-dashed fold meets the first red fold. These two lines are marked in green in the image.

Your angle is now trisected. The last two lines you drew cut the original angle into 3 smaller angles, all equal.

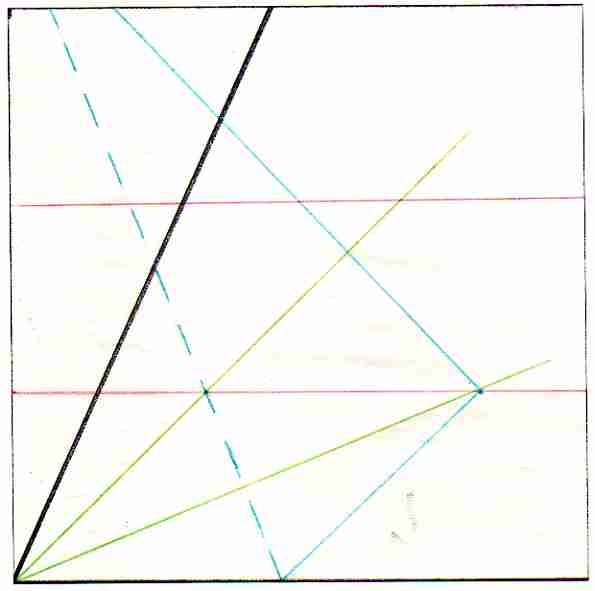
Can You Prove It?

Folding paper is the easy part, but now your hard work begins.

• How can we know that this method trisects the angle?

Any mathematical proof starts with some set of given facts.

• Look again at the first patty paper image.
• What do you know for sure about those lines? Make a list!

In order to write down what you know, you will have to give names to some of the points and lines in the drawing. Either print out the image and write on it, or make a sketch of your own.

Then look at the second image.

• Is there anything you know for sure about the new lines?
• How do you know it?
• Write down any facts you can think of, and be sure to include a reason for each fact.

Now concentrate on understanding what you are trying to prove.

• What exactly does it mean to trisect an angle?
• Can you write a mathematical statement or equation that means the same thing as, “This angle is trisected”?

Finally, you need to find a way to get from the facts you are given to the statement you want to prove, and you need to show a valid reason for each step along the way. Think back to the things you learned in math class.

• What do you know about triangles?
• What do you know about parallel lines?
• Will any of those facts help you here?

If You Get Stumped

Later today, I’ll post a follow-up article with a few hints, and that will be the place to share your questions or proofs, if you wish. Comments here below are limited to general remarks that won’t spoil anyone else’s fun in working through the puzzle.

UPDATE: The hints post is here.