Mental Math: Advanced Division

The farther we go in math, the more division disappears. It ceases to exist as a separate concept.

Instead, we learn to see division as:

• an inverse multiplication
• a fraction (ratio)
• a proportional relationship

Each of these perspectives offers us a new way to think about and make sense of our calculations.

Check the Factors

Division is the inverse of multiplication, so if one number divides perfectly into another number, you’ll be able to find all the factors of the smaller number inside the larger one.

For example: 300 ÷ 15 =?

Or in other words, “What number times 15 gives 300?”

300
= 3 × 100
= 3 × (10 × 10)
= 3 × (2 × 5) × 10
= (3 × 5) × (2 × 10)
= 15 × 20

So 300 divided by 15 is 20.

Division Makes a Fraction

Isn’t it funny how all the really tough topics in math are just fractions in disguise?

Any division problem can be written as a fraction, reading from top to bottom like the page of a book: numerator divided by denominator.

Then you can scale that fraction down to its simplest form which is the answer to your division calculation.

Looking again at 300 ÷ 15:

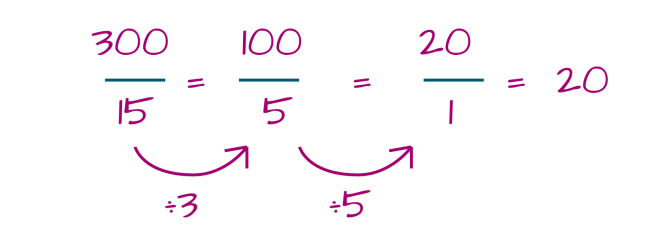
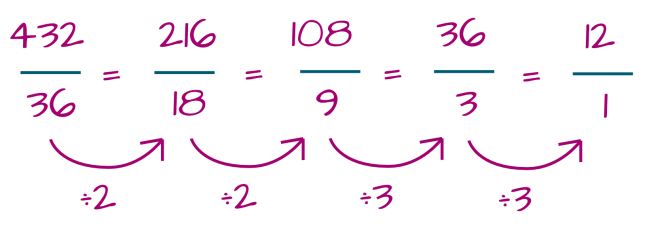
Or what is 432 divided by 36?

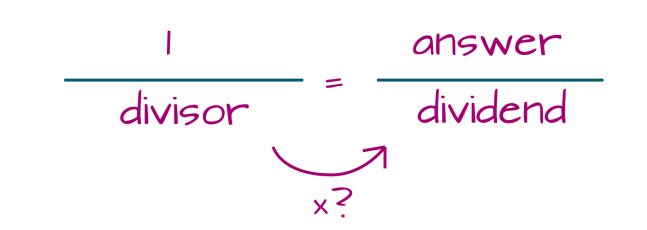
If you forget which direction the division fraction goes, you can figure it out by thinking of pizzas:

2 pizzas divided by 3 teenagers
= 2/3 pizza per person

Use a Ratio Table

Again, we use the principle that division is the inverse of multiplication. We can start a ratio table with one of whatever we’re dividing by and scale up to get the number we want.

So we see division as a type of proportional relationship between the dividend (the number we are dividing) and its divisor (the divided-by number).

To see how it works, let’s go back to our chickens. If we’ve gathered 168 eggs, how many dozen do we have?

168 ÷ 12 = ? (What times 12 gives 168?)

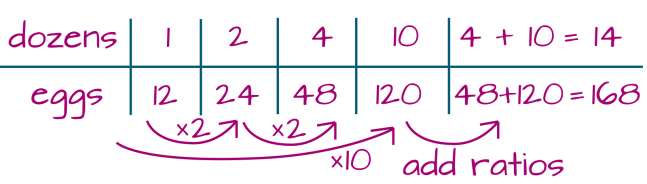
We have 14 dozen eggs, which give us 14 full egg cartons.

Beware of Remainders

In elementary division problems, a student often comes up with a quotient plus a remainder.

As we move into advanced division, remainders turn into fraction, and we must be careful to interpret what the fraction actually means.

For example, what if we gathered 230 eggs from our hens? How many cartons can we fill?

230 ÷ 12 =?

Let’s use the fraction method:

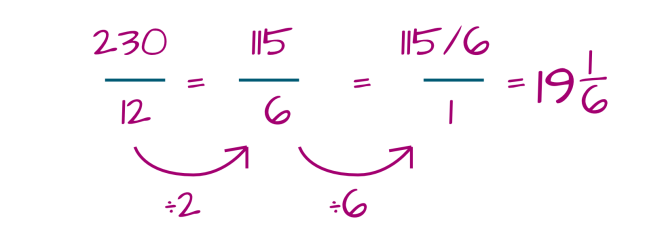
But can a hen lay 1/6 of an egg? No, remember we are counting dozens:

230 eggs ÷ 12 eggs per dozen = 19 1/6 dozens

We can fill 19 cartons plus part of the next carton. That last carton, only one-sixth full, must contain:

1/6 × 12 = 2 eggs.

What If It’s Too Hard?

Mental math can take us a lot farther than most people think.

The more time our children spend playing around with numbers and making sense of these relationships, the better they’ll be prepared for algebra and beyond.

But for a high school chemistry student, or an adult filling out their tax forms, there’s no shame in using a calculator or spreadsheet. Use the proper tools for each task. When the important thing is to get a correct answer, use technology.

On the other hand, when the important thing is learning, developing a student’s understanding and mastery of arithmetic relationships as preparation for future study — well, what better tool for that than mental math?

“If you stay with meaningful mental arithmetic longer, you will find that your child, if she is average, can do problems much more advanced than the level listed for her grade. You will find that she likes arithmetic more. And when she does get to abstractions, she will understand them better.”

—Ruth Beechick, An Easy Start in Arithmetic

Read the Whole Series

This post marks the end (at least for now) of my Mental Math Series:

• Mental Math Is the Key to Algebra
• Three Basic Principles
• Early Addition
• Early Subtraction
• Early Multiplication
• Early Division
• Advanced Addition
• Advanced Subtraction
• Mental Math Do’s and Don’ts
• Advanced Multiplication, Part 1
• Advanced Multiplication, Part 2
• Advanced Division