Homeschool Memories: Putting Bill Gates in Proportion

Once upon a time…

We were getting ready for the annual homeschool co-op speech contest, and a friend emailed me for help.

“Can you help us figure out how to figure out this problem?

“This is related to C’s speech. I think we have all the information we need, but I’m not sure:

“The average household income in the United States is $60,000/year. And a man’s annual income is $56 billion.

“Is there a way to figure out what this man’s value of a million dollars would be, compared to the person who earns $60,000/year? In other words, I would like to say—$1,000,000 to us is like 10 cents to Bill Gates.”

We found out later that her son’s numbers weren’t exactly right. He hadn’t understood the difference between income and net worth, so he made Gates sound richer than reality.

But the basic math principles never change, and it’s fun to play with big numbers.

This Is a Ratio Problem

More specifically, to solve this problem we need to write a proportion, which means one ratio is equal to another.

Here are a few things you need to know about ratios…

(1) A Ratio Is a Fraction

A ratio is simply a fraction comparing two numbers: “Numerator is to denominator.”

In this case we are looking at the ratio of the average income to the huge income, so:

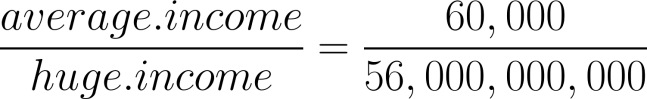
And we also want to compare spending money:

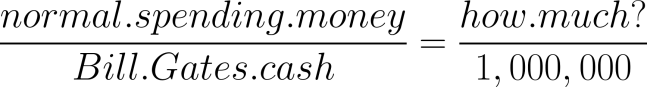
(2) Proportions Are Equivalent Fractions

A proportion says that one ratio is equal to another ratio.

In a proportion, you need to be sure you are comparing similar things in the same order.

You can arrange any proportion in different ways, some of which are easier to solve than others. It is always nice to try to get your proportion so that your unknown number is in the numerator of one of the fractions.

For example, if we assume that our free cash is in proportion to our income, we might figure:

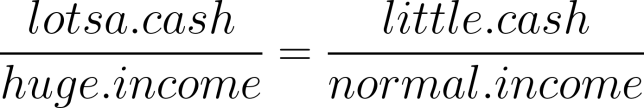
Or we could write:

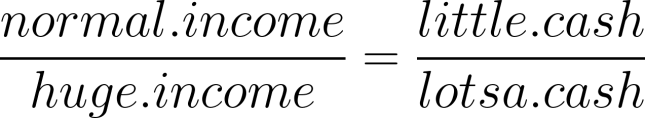
The main point is, you must always set both sides of the proportion so that similar thing compares to similar thing in the same order.

I will use the proportion, “Little income compares to huge income as little cash compares to Bill Gates’ spending money.”

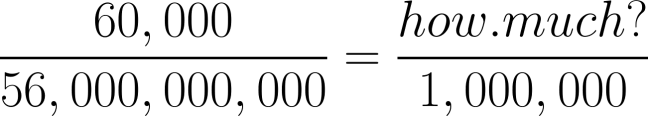
(3) Use What You Know

After you get the proportion set up the way you want it, you need to solve for your unknown number. Use what you know about fractions to figure it out.

The proportion says that these fractions are equivalent, so our unknown value must be whatever it takes to make them equal.

In this case, let’s simplify the fraction on the left so we can compare millions to millions:

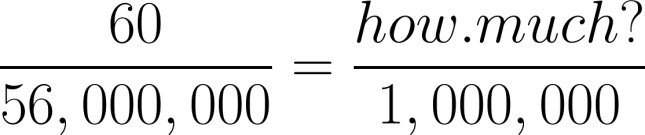
Now it’s easy to see how the denominators are related to each other. All we need to do is divide the numerator by the same amount:

60 ÷ 56 = our spending money = $1.07.

So a million dollars is to Bill Gates about the same as $1 to you and me.

Does That Make Sense?

“Absolutely! So, C can say that $1,000,000 to Bill Gates has the same value as $1 does to us? “If he flips it, that $1 to Bill Gates is like $1,000,000 to us, I think that would confuse the audience because it sounds as if we have more money than Bill.

“Or am I too confused?”

You are a little confused. The first thing you said is right, the “flipped” one is wrong. To Bill Gates, $1 million is pocket change. It is about the same as a buck is to us.

And to Bill Gates, $1 would not even be worth noticing. It would be about like $ 0.000001 would be to us. That is about 1/10,000 of a cent.

I have heard speakers use an analogy like this: If Bill Gates were walking down the street and saw a $100 bill on the ground, it would not be worth his time to pick it up. Compared to his net worth, that would be like one of us bending down to pick up 1/100th of a penny.

Of course, even Bill Gates could probably think of some use for a spare $100, right? Leave it as a lunch tip, or something.

The “Real World”

After our email chat, I looked up Bill Gates on Wikipedia and discovered $56 billion was his net worth, not his income. His salary at that time was $966,667/year. Even assuming he had significant investment income, that’s still a difference of several orders of magnitude.

Okay, so what should the calculation be, really? Let’s guess that Bill Gates’ investment income was about triple his salary income. I have no idea if that is accurate, but I couldn’t find any data online, and at least the assumption gives us something to work with.

Rounding everything off would give us a total annual income of about $4 million.

In that case, $1 million would be about one-fourth of Gates’ annual income, and the equivalent for a worker earning $60,000 is:

60,000 ÷ 4 = 15,000

And a $100 bill would be like $1.50 to us. That is still a big difference in perspective, but it sure doesn’t make the same impression in a speech.

What If the Proportion Isn’t So Easy?

These fractions came out fairly simple to work with. We could see how the denominators were related, so all we had to do was multiply the numerators by the same amount.

Proportions are always equivalent fractions, but it’s not always easy to see how they relate.

Your teachers may have told you to “cross-multiply” proportions, but that phrase is problematic because students forget what it means.

But there is magic in the equal sign of an equation: If any two fractions (or other mathematical expressions) are equal, then all their multiples must be equal as well.

If two numbers are equal, then their doubles are equal. As are their triples, and their seven-tiples, and any other multiple. We can always multiply both sides of the equation by the same amount, and the new equation will remain true.

So, we can always multiply both sides of our proportion by the denominator under our unknown number. That will give an equation with the unknown equal to some calculation—the original fraction times the other denominator—so then we only need to do that calculation to solve our proportion.

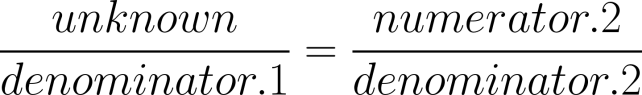
As long as we arrange our proportion with the unknown number in the numerator, we can just crank the numbers through our calculator to solve it.

And since the key to working with proportions is to compare similar thing to similar thing in the same order, we can always arrange that order to suit our preference. We can always get the unknown on top.

What If the Unknown Isn’t on Top

Your textbook or teacher may try to trick you by giving a proportion that’s not arranged the right way. If so, you can easily change it to get the unknown on top.

Just remember a simple truth about fractions:

If a/b = c/d,

Then it must also be true

That b/a = d/c,

Always and forever. Amen.

If two numbers are equal, then their reciprocals have no choice but to be equal as well. It’s a principle built into the very nature of numbers.

Test it for yourself by making up some equivalent fractions and then flipping them. It always works!

So you just need to flip both fractions of the proportion. The flipped versions will still equal each other, and with the unknown on top, you’ll be able to make sense of solving it.

Try It for Yourself

Bill Gates is old news now. So here’s a journaling prompt for you:

Research Elon Musk, or any other billionaire of your choice. Find out what you can about his earnings and compare it to today’s average family income.

If Elon Musk spent a million dollars, how much would a normal person spend in the same proportion? Or if Musk found a $100 bill on the sidewalk, what would be the equivalent in cash to us?