Mental Math: Advanced Multiplication, Part 2

The methods in last week’s Advanced Multiplication post only work for certain numbers, but we have another, more powerful multiplication tool: We can always use a ratio table to make sense of any multiplication.

Ratios are the beginning of proportional thinking. We can systematically alter the numbers in a ratio to reach any quantity required by our problem.

Students begin working with ratios in story problems that help them visualize and make sense of a proportional relationship.

Ratio Tables

For example, last spring’s chickens are laying now, supplementing the supply from our older hens. We store the eggs in dozen-cartons, and our refrigerator is starting to overflow.

What calculations might we do with the ratio of eggs to cartons?

We write a ratio table horizontally or vertically, one row (or column) for the cartons, and another for the eggs.

Then we fill in additional entries by multiplying or dividing both numbers by the same amount, just like making equivalent fractions.

We can play with the powers of two.

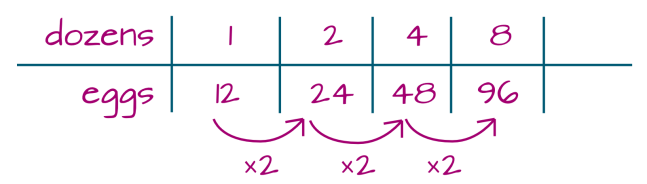
So, 8 cartons contain 96 eggs.

We can scale the ratio up (multiply) or scale it down (divide) by anything we like, doing the same thing to both rows, keeping them in proportion.

Let’s play with 5 and 10:

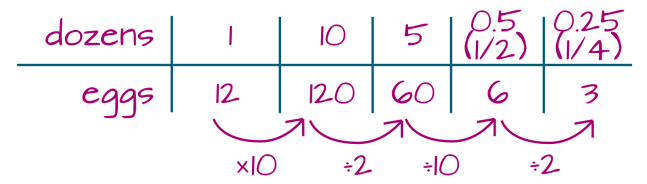
So, there are 60 eggs 5 dozen, and a quarter-dozen is only 3 eggs.

More Ways to Play

Here is a tip for using ratio tables in more complex situations:

You can add two ratios together by adding the tops to get a new top number and adding the bottoms to get a new bottom number.

Yes, just exactly how NOT to add fractions!

So, there are 108 eggs in 9 dozen.

It works because the parts stay in proportion:

• 1 dozen is 12 eggs.
• 8 dozen is 96 eggs.
• So it makes sense that (1 + 8) dozen will be (12 + 96) eggs.

Any time we add two ratio entries together in this way, each to its own part, we find a new set of numbers that maintain the same proportion.

For example:

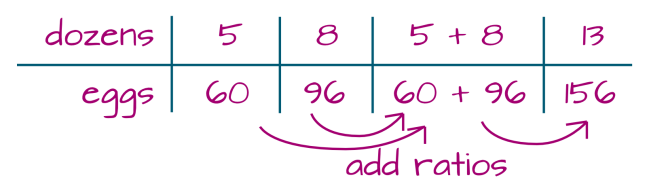
So, it would take 156 eggs to make 13 dozen.

Abstract Ratios

As students get used to working with ratio tables, they can move beyond story problems to reason proportionally about any numbers.

Even fractions:

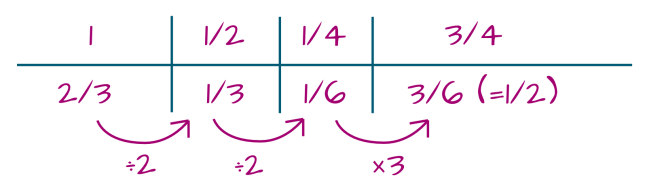
So, 3/4 of 2/3 is 3/6 (= 1/2).

Why Not Just Follow the Steps?

If we were only interested in getting correct answers, we could teach our children to follow the steps of the standard arithmetic algorithms. Many of our pupils might have trouble remembering all the different rules and struggle with confusion. But with enough drill and practice, most of them would manage to pick up most of the techniques. To some degree.

Answer-getting is happy for children to learn a method with only the vaguest idea why it works.

Real mathematics, however, is always about thinking and making sense.

These mental-math methods put the child’s focus on understanding and using number relationships, laying a firm foundation on which we may build future math concepts.

Besides, this sort of number play gives children the freedom to make choices and use their own creativity in math. There are so many ways to look at any number relationship, they don’t need to worry about guessing what the teacher wants. Anything goes, if they can show that it makes sense.

“This is one of the reasons why I push so hard against the multiplication algorithm.

“Because if the only thing you ever do is rote memorize a bunch of single-digit facts and then apply them in the multiplication algorithm, you never develop the distributive property. You never get to these associative property strategies, where you’re really factoring the factors in order to make an equivalent problem that’s easier to solve.

“That’s a big deal. Like, you haven’t filled out your multiplicative reasoning at all.

“Multiplicative reasoning is dense. It’s not just reasoning with single-digit facts and getting a bunch of answers. There’s more distributive property, kind of partitioning-the-factors thinking. And then there’s the more associative property, factoring-the-factors thinking.

“And we want to build that in kids, and we can. The answer is not only can we, but it’s fun.”

—Pam Harris, “Connecting Strategies, Properties, and Models in Multiplication”

Read the Whole Series

Check out all the posts in my Mental Math Series:

• Mental Math Is the Key to Algebra
• Three Basic Principles
• Early Addition
• Early Subtraction
• Early Multiplication
• Early Division
• Advanced Addition
• Advanced Subtraction
• Mental Math Do’s and Don’ts
• Advanced Multiplication, Part 1
• Advanced Multiplication, Part 2
• Coming Soon: Tips for advanced division…