Remember the Math Adventurer’s Rule: Figure it out for yourself! Whenever I give a problem in an Alexandria Jones story, I will try to post the answer soon afterward. But don’t peek! If I tell you the answer, you miss out on the fun of solving the puzzle. So if you haven’t worked these problems yet, go back to the original post. Figure them out for yourself — and then check the answers just to prove that you got them right.
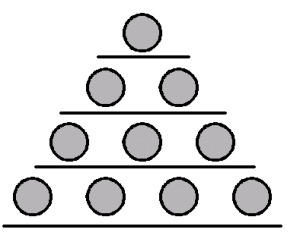
Triangular Numbers
(1) Can you find the pattern in the triangular numbers?
The rows of the triangle are consecutive natural numbers:
(2) If n stands for any number, can you write a formula to calculate the nth triangular number?
The nth triangular number is the sum of all the natural numbers from 1 to n. If your number n is very large, however, that addition may take more time than anyone is willing to spend. Instead, you need the triangular number formula:
[Editor’s note: Here are 3 ways to prove this formula. The triangular numbers are closely related to the handshake problem, which was featured in this post.]
Square Numbers
(3) Can you find the pattern Alex noticed?
To build each new square number, Leon added a backwards-L-shaped set of pebbles: a new base plus a new vertical column. Alex saw that each L-shape contained an odd number of stones, so each square number is the sum of consecutive odd numbers:
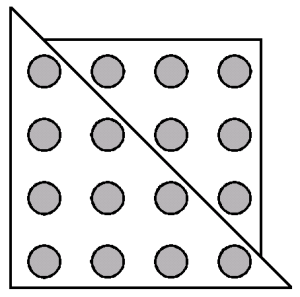
(4) Can you show that every square number is the sum of two triangular numbers?
You cannot divide the square number exactly on its diagonal without splitting pebbles in half. Look at the drawing, however, and you will see that each square number must be the sum of two consecutive triangular numbers:
Do you see why this pattern will continue to be true as the square grows?
(5) What 2-digit number is both square and triangular?
If you figured out the next several numbers in each set, you would find that:
(6) If n stands for any number, can you write a formula for the nth square number?
To find the nth square number, you could add up the first n odd natural numbers. This has the same nuisance factor as with the triangular numbers. Fortunately, the formula for the nth square number is simple:
Pentagonal Numbers
(7) How is each pentagon the sum of a square and a triangle?
As shown in the drawing, each pentagonal number is the sum of a large square [the square is distorted, but if you look carefully, you will see 4 rows of 4] and a smaller triangle:
Do you see why this pattern must continue to be true as the pentagon grows?
Now, since every square number is made of two triangles, we could also divide the pentagonal number into three triangles — one large one and two smaller. Can you find them on the drawing?
(8 ) If n stands for any number, can you write the formula for the nth pentagonal number?
The pattern for the pentagonal numbers is: 1 + 4 + 7 + 10 + …, each time adding 3 more than the time before. To calculate the nth pentagonal number without adding up all the pebbles:
(9) Can you find a number that is both triangular and pentagonal? How about a 4-digit number that is both square and pentagonal?
If you cranked out a whole list of numbers, you would find that:
…and…
Better yet, set up a spreadsheet to do the calculations for you. That is good practice in “real-life” math, since many jobs will require you to be spreadsheet literate. Maybe you can even convince your teacher to count it as an extra-credit math project.
(10) Did you find the pentagonal square triangular number?
According to Wolfram MathWorld, there is almost certainly no number that is triangular and square and pentagonal, except for:
To Be Continued…
Read all the posts from the March/April 1999 issue of my Mathematical Adventures of Alexandria Jones newsletter.


how do you get the rule for the rule of any type of number e.g. triangular,pentagonal, hexagonale.t.c
The easiest way to find a formula — at least, if you are a visual thinker, like me — is to break the pattern down into a sum of squares and triangular numbers, as I did above. Then write those formulas, being careful to put (n-1) or (n-2) or whatever in all the right places. Simplify the resulting equation with basic algebra.
For a more general approach, you could look at this explanation.
Nice site! 🙂 We just posted it at
http://forums.delphiforums.com/figurate/start
there really is no easy way to find a formula. well first you need to plug variables in for all the things you’re trying to find, ONLY THEN can u see the formula.