
[Photo by pfala.]
Did you know that playing games is one of the Top 10 Ways To Improve Your Brain Fitness? So slip into your workout clothes and pump up those mental muscles with the 2010 Mathematics Game!
Here are the rules:
Use the digits in the year 2010 to write mathematical expressions for the counting numbers 1 through 100.
- All four digits must be used in each expression. You may not use any other numbers except 2, 0, 1, and 0.
- You may use the arithmetic operations +, -, x, ÷, sqrt (square root), ^ (raise to a power), and ! (factorial). You may also use parentheses, brackets, or other grouping symbols.
- You may use a decimal point to create numbers such as .1, .02, etc.
- Multi-digit numbers such as 20 or 102 may be used, but preference is given to solutions that avoid them.
Bonus Rule
You may use the overhead-bar (vinculum), dots, or brackets to mark a repeating decimal.[Note to teachers: This rule is not part of the Math Forum guidelines. It makes a significant difference in the number of possible solutions, however, and it should not be too difficult for high school students or advanced middle schoolers.]
How Does It Work?
Use the comments section below to post a running list of the numbers you have been able to calculate. You may also share relatively cryptic tips and hints, but be warned: Some teachers use this puzzle as a classroom assignment, and there will always be students looking for people to do their work for them.
Do not post your solutions. I will delete them.
I know of no authoritative list of numbers that can be made with each year’s digits, so we will rely on our collective wisdom to decide when the game is done. We had a lively discussion the last few years. I’m looking forward to the fun!
Keeping Track
As the game results are reported below, I will keep a running tally of confirmed results (that is, numbers reported by two or more players). Today is Kitten’s birthday, however, and we have company coming in for the weekend, so this tally will lag a few days behind the results posted in the comments.
Percent confirmed = 74%.
Numbers we are missing =
34, 38, 43, 47, 52, 56, 58, 62, 66-69, 74, 76-78, 84-87, 89, 91, 93-96.
And if you would like to join me in the “extended edition” game…
Found an expression *without* multi-digit numbers:
1-13, 15-33, 35-37, 39-41, 44-46, 48-51, 53-54, 59-61, 63-65, 70-73, 75, 79-83, 90, 99 and 100.Found a way to keep the digits in order:
1-13, 16, 18-26, 27-33, 36, 40, 49-51, 53-54, 59-61, 64, 70-73, 88, 92 and 97.
Update: Math Forum has posted their 2010 Student Solutions page. Since they did not allow repeating decimals, their list of solutions is a bit shorter than ours.
Helpful Links
- 2010 Mathematics Game Worksheet
For keeping track of which numbers you’ve solved.
- 2010 Mathematics Game Manipulatives
This may help visual or hands-on thinkers.
- 2010 Mathematics Game Student Submissions Information
For elementary through high school students who wish to share their solutions, to be posted beginning February 1st.
Clarifying the Rules
Finally, here are a few things that some players have found confusing in past years:
- By definition:
. [See Dr. Math’s Why does 0 factorial equal 1?]
- For this game we will accept:
. [See the Dr. Math FAQ 0 to the 0 power.]
- Unary negatives are allowed. That is, you may use a “-” sign to create a negative number. This is particularly helpful if you are trying to keep the digits in 2-0-1-0 order.
- The only digits that can be used to build 2-or-more-digit numerals or decimals are the standard base-10 digits 2, 0, 1, 0.
- “0!” is not a digit, so it cannot used to create a base-10 numeral.
- The decimal point is not an operation that can be applied to other mathematical expressions: “.0!” does not make sense.
- No exponent may be used except that which is made from the digits 2, 0, 1, 0.
- You may not use a square function, but you may use “^2.”
- You may not use a cube function, but you may use “^(2+0!).”
- You may not use a reciprocal function, but you may use “^(-0!).”
- You have to “hit” each number from 1 to 100 exactly — no rounding off or truncating decimals allowed. You may not use the integer function.
For more hints, check out this comment from the 2008 game.
I went back to bed, and thought about the first few. I have one for each of the days of January, that’s 1 – 31.
14 was the hardest for me.
I won’t have much more time before next week.
Jonathan
My company went to visit other relatives for a bit, so I had a little time to work. I can confirm 1-31, except for #17, 27, 28 — haven’t found those yet.
I also found: 36, 40, 42, 45, 49-51, 55, 59-61, 70, 71, 81, 98, 100.
I had to use 2-digit numbers for: 13, 14, 16, 42, 45, 55, 98.
I could NOT get the digits in order for: 13-16, 42, 45, 55, 70, 81, 98, 100.
I wonder if I could find my notes from last year. There might be a few useful expressions there…
i found 46 numbers, 1-25 has been found, i can’t find 17 though…
I have 1 – 32
also 35 – 37
40, 42, 44- 46, 48-51
53-55, 57, 59-61
63-65 and then it gets spotty
70, 72, 80-82, 88, 90, 92, 98 -100
I’ve got 43/100 so far. I’m missing several numbers from JD’s list, but I verify 71 from Denise’s list, and add 73 for potential verification. (I got 71-73 with the same trick)
I’m starting this with my math classes tomorrow, and am trying to decide how successful I can expect my students to be with it. The lack of any larger single digits is making this very tough, as I’m sure everyone knows. I know that I’ll have some students who can be very successful with it, and others who will probably struggle to get 15 or 20 numbers.
Wow! Jonathan has obviously found a few tricks I haven’t. I’m missing MANY on his list. I did find 33, which I don’t think anyone has mentioned yet.
Okay, I will mark the following numbers as confirmed so far (49%): 1-16, 18-26, 29-32, 36, 40, 42, 45, 49-51, 55, 59-61, 64, 70-73, 81, 98-100.
Reported as possible, but not confirmed: 17, 27, 28, 33, 35, 37, 44, 46, 48, 53-54, 57, 63, 65, 80, 82, 88, 90, 92.
From the confirmed list, I am missing 26 and 42…not sure what the trick is for those, but I’m plugging away…nothing else to add to the list yet…I must be missing the same tricks Denise, because JD still reports many that I can’t even touch.
I start to get paranoid when I look at these sometimes, thinking I’m missing some obvious trick that will make a breakthough. I probably spent far too much time yesterday trying to figure out how to make three from 1 and 0…
My first class of the day had a blast with this, and by the end of the period had collectively found 29 numbers, which I thought was a great success for the time I was able to give them. I’m eager to see how many stick with it and wow me with more answers. Two more classes will start it today, and 1 more tomorrow, so we’ll see how that goes.
26 was a tricky one, but I managed to make 25 with only the 2,0,1, so I had an extra digit to add at the end. 42 is slap-the-forehead easy, if you use a 2-digit number.
So, did you figure out a way to make 3 from the 1 and 0? If you did, I’d like a hint on how. That would really help!
Back to “school” today, Kitten decided this puzzle was more fun than her regular math homework. I had to explain factorials to her and remind her how exponents work. So far, she’s found the numbers 1-8, which isn’t a bad start for a 5th grader. Before she goes back to it, I’ll remind her that she doesn’t have to look for the numbers in order, and that she can use 2- or 3-digit numbers, too. That will quickly add several more to her list.
I caught up on 71 and 73.
Yesterday in class I got 97, which is quite tricky.
I can confirm that all of those I have that you do not used the same maneuver.
Jonathan
Ah, no the 1+0=3 trick was just wishful thinking (so far anyway). Thanks for the help with 26 and 42. You were definitely right that 42 was “slap-your-forehead easy”. 26 took me a little bit, but I figured it out too. No progress on any of JD’s extra numbers yet, but I’m still mulling it over.
The rest of my classes seem to have really enjoyed the day of “recreational mathematics.” Whether they saw it as a slack-off day, or just a change of pace, I can’t testify too, but I know I managed, at least, to hook several students each hour. I think if I get any more appreciation of math in their lives, it will have been a success.
Ah, I see Jonathan’s trick. We have discussed that in the past, but we never allowed it because it doesn’t fit the Math Forum rules. This year, however, it makes such a HUGE difference (and it’s certainly not too difficult for high school students or advanced middle school) that I think I will make an exception:
Bonus Rule
You may use the overhead-bar (vinculum), dots, or brackets to mark a repeating decimal.
And with that modification of the rules, I can verify all of Jonathan’s numbers and add the following: 39, 41, 75, 79, 83.
oops, didn’t remember it not being ok. Certainly I don’t know how to finish 4 fours without it, and assumed it just carried over.
Hmm. That’s probably one of the reasons I’ve never managed to finish 4 Fours.
At any rate, we will certainly allow it this year, and probably in the future, too. I didn’t use it before, because I first heard of this game through Math Forum, and they don’t mention it. But it’s a nice addition.
Wow, that bonus rule WAS really helpful. I’m not quite caught up yet, but I’m rapidly making progress. Also, I can confirm 39, 75, 79, and 83 from your list.
I assumed 41 would be a tweak of how you got 39, but if so, then I found a different method than you did.
I found 40 three different ways, the last of which gave me an extra digit to adjust for 39 and 41. I did not find an independent expression for 39.
Updated stats:
Percent confirmed = 72%.
Reported as possible, but not confirmed: 33, 41.
Numbers we are missing =
34, 38, 43, 47, 52, 56, 58, 62, 66-69, 74, 76-78, 84-87, 89, 91, 93-96.
I can confirm 33 and 41.
I used repeating decimals for the following numbers: 17,27,28,33,35,37,39,41,44,46,48,53,54,57,63,65,75,79,80,82,83,88,90,92,97
Are any of these possible without the bonus rule?
OMG I am so happy I found your blog. I have a 6 yr old who is in school. He is having a difficult time in math. The concepts they use are NOT working. The games you have he will love! He gets so frustrated he cries. It’s so sad. I get frustrated because his teacher just pushes him. They change concepts all the time. He barely wraps his brain around one concept before they switch. It’s irritating. When I asked his teacher for advice she told me to keep working with him and there was no *magic* formula. GRRR…Nice teacher, huh?
Corrie,
From your list, I got 33 without the bonus rule.
Imperfect Me,
Thanks for visiting, and I’m glad you’ve enjoyed my blog. I hope you aren’t planning on playing this game with your 6yo! Better to try some of my early-elementary posts.
i only have 24% of the answers i am having a lot of trouble. can anyone help me with some
With only three distinct digits to work with this year, you will have to use every trick in the book to create variety in your numbers. Especially, you will want to play around with:
* Double-digit numbers.
* Factorials, and factorials of factorials.
* Decimals, which are very important this year.
Remember also that dividing or using a negative exponent creates the reciprocal of a fraction, which can flip the denominator up where it can be more helpful.
I found some additions for the extended version of the game (but not 33, though):
without multi-digit numbers you can do 90, 99 and 100
with digits in the right order: 16, 88, 92 and 97
Thanks, Corrie! I’ll add those to my list. I’ve been swept away with busy-ness as school got back into session, but I hope to find some time this weekend to puzzle at this some more.
thanks for posting this problem
i’ve put it up on our challenge problem board to do
numbers up to 31 (number of days in january)
some questions, while you mention .0! as not a valid substitute for .1
wouldn’t .(0!) be allowed?
in your list of missing numbers are those allowing the repeating decimal operation and multiple digit numbers?
allowing such use of brackets and using repeated decimals but no multiple digit numbers I have 1 to 31 using 2,0,1,0 in order
up to 100 ,using some multidigit numbers, i’m missing 38,43,47,48,52,56,58,68,69,74,76,85,86,87,89,93,94,95,96
thanks again
ron
I think the restriction, stated in English, is that it is not permissible to create a number, and then use that result as a digit in a number.
So, using a 3 and a 0, we couldn’t make 60 by taking 3! and putting a zero after the result.
So .(0!) would involve creating a 1, then using it as a digit in another number, which is not permissible.
Jonathan
Jonathan is right. Only the actual digits of the year (2,0,1,0) may be used to create decimal or multi-digit numbers. It just doesn’t make sense to write something like (2+1)0 and call it 30.
The only place I could imagine doing that would be on a place value chart with young students, where one is teaching about the columns and treating each column separately. (For instance, to show that 20+10 is 2+1 tens.) But you can’t write free-standing numbers that way.
hi jd/denise
i don’t think you have addressed the question i asked
certainly creating a multidigit number using previously created single digits is not allowed
i just wanted clarification on whether .(0!) could be used as .1 which seems okay?
Hi, Ron! I’m sorry my reply wasn’t clear.
No, you cannot say that 0!=1 and then take that and put a decimal point next to it. “.(0!)” is not the same as “.1”—the only way you can make “.1” is to use the digit 1 from your original digits (2,0,1,0).
Similarly, saying “2(0!)” is not the same as “21”, and “1(0!)2” can’t be used for “112”, and “.0(0!)” does not make “.01”, and etc. You just can’t write numbers that way.
Denise
the problem involves operations on the numbers 2,0,1,0
if you don’t allow .(0!) as .1 then you are forbidding successive operations, in this case take factorial then create the decimal
under such a restriction then taking factorial twice once 3 is obtained, such as (2+1)!! should also not be acceptable
likewise the square root of .111… would also not be allowed as it amounts to the successive operations: create the repeating decimal using the digit 1 followed by square root
are you really sure you want to stick with these rules (i.e. you can’t do successuive operations on a number once created) or have i misunderstood that you are free to use the operations repeatedly?
PS
your example of trying to create 21 as 2(0!) is in no way similar to using .(0!) as .1 (other than using 0! as 1)
No, Ron. The decimal point is NOT an operation. There is no such thing as a “create the decimal” operation.
You may do successive operations — as many as you wish! — but you may not insert a decimal point after doing an operation.
thanks for the clarification
does it imply that the only decimals allowed are .1 and .2 and their infinitely repeated versions for 1/9 and 2/9 (or if multiple digit numbers allowed .01, .201 etc with repeated versions) so in essence you allow an initial operation of create .? for ? a (multidigit) number using 2.0.1,0 (and .??????…in extended rules)
i’m okay with that as a restriction but ‘operation’ is a slippery concept and creating .n from a given natural number n is a valid operation just not a standard operation- you can’t empirically claim it is not an operation but you can for this particular activity
it spoils my liat of using the digits in order such as
30= 2 divided by .(0!) + 1 divided by .(0!)
and will need to settle for 2 divided by .1 + 0! divided by .1
BTW: Math Forum has posted the student solutions.
Just read something about double factorials (!!). Are they allowed?
Why not? I had never heard of them before, but now that John has enlightened us, we might as well play around with them.
To clarify:
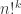 = product of all integers from 1 to n that are equal to n mod k, where both n and k must be constructed from the year digits
= product of all integers from 1 to n that are equal to n mod k, where both n and k must be constructed from the year digits
(n!)! = a factorial of a factorial
n!! = a double factorial = the product of all integers from 1 to n that have the same parity (odd or even) as n
n!!! = a triple factorial = the product of all integers from 1 to n that are equal to n mod 3
Now that I’ve done a search and realized how many different kinds of factorials there are, I think we need to draw a line somewhere. So let’s allow multifactorials (with the above limitation regarding n and k) but not subfactorials, superfactorials, hyperfactorials, alternating factorials, primorials, etc.
I won’t have time to play with the numbers for several days, but I look forward to hearing what you discover….