Mental Math: Early Division

Mental math is doing calculations with our minds, though we can use scratch paper or whiteboards to make notes as we work.

Doing mental math, children use the basic principles of arithmetic to simplify problems so they can think about number relationships, mastering the basic structures of how numbers work, the same structures that underlie algebraic reasoning.

As always, we rely on two key mental-math strategies.

• Use friendly numbers.
• Estimate, then adjust.

Division is the mirror image of multiplication, the inverse operation that undoes multiplication, which means we are scaling numbers down into smaller parts. Important friendly numbers include halves, thirds, and tenths, plus the square numbers and any multiplication facts the student happens to remember.

Let’s Try an Example

For instance, how might children think through a subtraction puzzle such as forty-two divided by six? As the inverse of multiplication, this problem asks, “Six times what makes forty-two?”

42 ÷ 6 = ?

Means the same as:

42 = 6 × ?

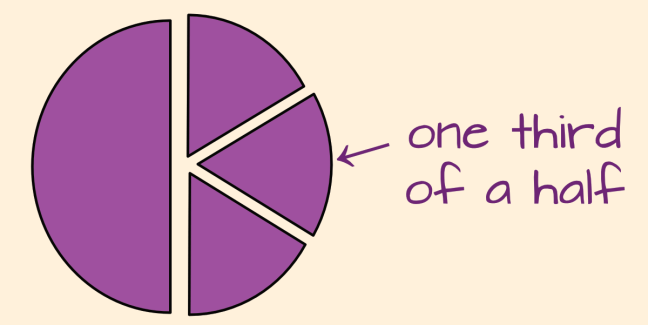
Half Then Thirds

We know that six is two times three, so to multiply by six we can scale up by two and then by three: double the number and triple that amount.

To divide by six, we do the reverse: find half of the number, and then find one-third of that amount. Half of 42 is 21, and one-third of 21 is 7.

Think:

6 = 2 × 3

So:

42 ÷ 6 = 42 ÷ 2 ÷ 3

= 21 ÷ 3 = 7

Friendly Squares

The square numbers often come in useful with hard-to-remember multiplication or division facts.

In this case, six squared is thirty-six, which isn’t quite big enough. Adding one more six makes thirty-twelve, the same as forty-two.

Think:

42 = 36 + 6

 = (6 × 6) + (1 × 6)

So:

42 ÷ 6 = 6 + 1

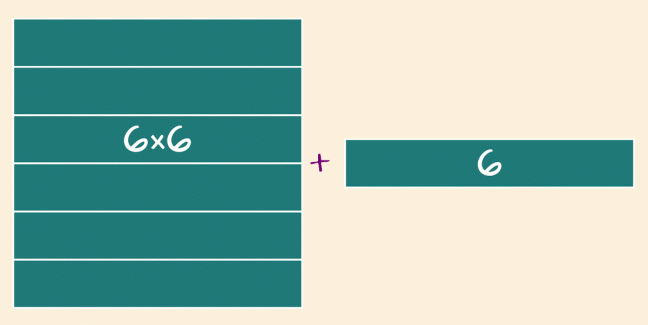
Other Friendly Parts

Splitting a number into smaller pieces can make for an easier calculation.

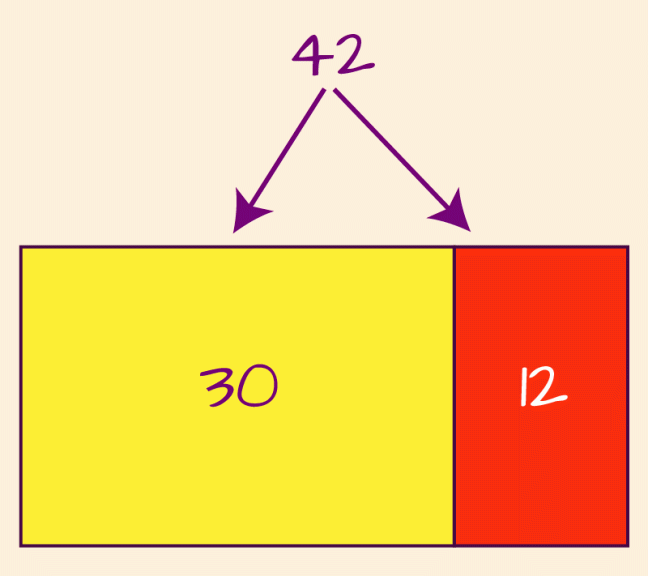
We could use the distributive property to split forty-two into smaller chunks that we know how to divide. Forty-two is thirty and twelve more, which is five sixes and two more sixes:

Think:

42 = 30 + 12

 = (5 × 6) + (2 × 6)

So:

42 ÷ 6 = 5 + 2

Friendly Doubles

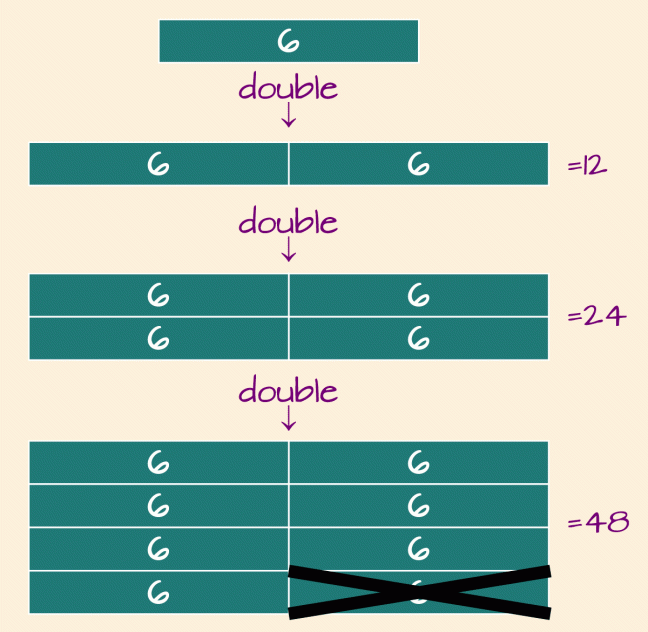
Doubles and halves are the absolute friendliest of multiplication and division problems, the first calculations young children begin to play with. Can we count up how many sixes there are in 42 by doubling?

Two sixes make twelve.

Doubling that gives us four sixes = two twelves = twenty-four.

Doubling one more time will make eight sixes = two twenty-fours = forty-eight.

Oops! That’s too big, so we need to take back one of the sixes.

Think:

2 × [2 × (2 × 6)]

 = 48 = 8 × 6

48 − 6 = 42

So:

42 ÷ 6 = 8 − 1

Can you think of any other ways to reason through 42 ÷ 6?

The more time you and your children spend playing with numbers and their relationships, the stronger their understanding will grow.

Read the Whole Series

Check out all the posts in my Mental Math Series:

• Mental Math Is the Key to Algebra
• Three Basic Principles
• Early Addition
• Early Subtraction
• Early Multiplication
• Early Division
• Coming Soon: Advanced mental math strategies…