From Numberphile: “Some stuff about Pi, the ‘celebrity number’. This video features maths-loving author Alex Bellos and Professor Roger Bowley from the University of Nottingham.”
Did you notice the error? It was supposed to be “a”…
Blog
Math Teachers at Play #83 via CavMaths
The new Math Teachers at Play math education blog carnival is up for your browsing pleasure. Each month, we feature activities, lessons, and games about math topics from preschool through high school. Check it out!
[Photo by Steve Bowbrick. (CC BY 2.0)]
Hello, and welcome to the 83rd Edition of the monthly blog carnival “Math(s) Teachers at Play”.
It is traditional to start with some number facts around the edition number, 83 is pretty cool, as it happens. Its prime, which sets it apart from all those lesser compound numbers. Not only that, its a safe prime, a Chen prime and even a Sophie Germain prime, you can’t get much cool than that can you? Well yes, yes you can, because 83 is also an Eisenstein prime!!!!
Those of you who work in base 36 will know it for its famous appearance in Shakespeare’s Hamlet: “83, or not 83, that is the question…..”
Playful Math Snacks: Why Pi?
Teachers and other math nerds are preparing to celebrate an epic Pi Day on 3/14/15. Unfortunately, the activities I see on teacher blogs and Pinterest don’t include much actual math. They stress the pi/pie wordplay or memorizing the digits.
With a bit of digging, however, I found a couple of projects that let you sink your metaphorical teeth into real mathematical meat. So I put those in the March “Let’s Play Math” newsletter, which went out this morning to everyone who signed up for Tabletop Academy Press math updates.
If you’re not on the mailing list, you can still join in the fun:
A Preview
Math Snack: Why Pi?
In math, symmetry is beautiful, and the most completely symmetric object in the (Euclidean) mathematical plane is the circle. No matter how you turn it, expand it, or shrink it, the circle remains essentially the same. Every circle you can imagine is the exact image of every other circle there is.
This is not true of other shapes. A rectangle may be short or tall. An ellipse may be fat or slim. A triangle may be squat, or stand up right, or lean off at a drunken angle. But circles are all the same, except for magnification. A circle three inches across is a perfect, point-for-point copy of a circle three miles across, or three millimeters…
The Math Student’s Manifesto
[Feature photo above by Texas A&M University (CC BY 2.0) via Flickr.]
Note to Readers: Please help me improve this list! Add your suggestions or additions in the comment section below…
What does it mean to think like a mathematician? From the very beginning of my education, I can do these things to some degree. And I am always learning to do them better.
(1) I can make sense of problems, and I never give up.
- I always think about what a math problem means. I consider how the numbers are related, and I imagine what the answer might look like.
- I remember similar problems I’ve done before. Or I make up similar problems with smaller numbers or simpler shapes, to see how they work.
- I often use a drawing or sketch to help me think about a problem. Sometimes I even build a physical model of the situation.
- I like to compare my approach to the problem with other people and hear how they did it differently.
Quote: Living Mathematics
Only dead mathematics can be taught where competition prevails: living mathematics must always be a communal possession.
— Mary Everest Boole
CREDITS: Today’s quote is from Mary Everest Boole. Background photo courtesy of State Library of Queensland, Australia (no known copyright restrictions) via Flickr.
Fun with the Impossible Penrose Triangle
I found this delightful animation today:
The ball is traveling around a shape that can’t exist in our real world: the Penrose triangle. This illusion is the basis for some cool art, like Escher’s Waterfall. And I’m using it in my Math You Can Play books as a design on the back of my playing cards:
Want to Play Around with the Penrose Triangle?
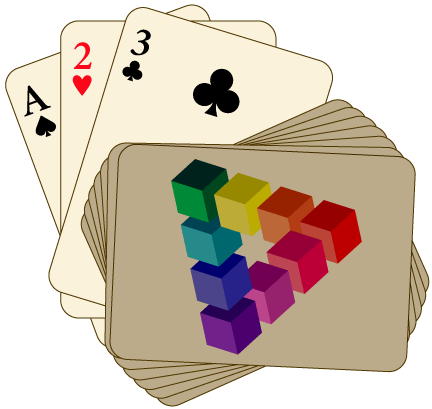
Here’s a few links so you can try it for yourself:
- How to Draw an Impossible Triangle
- Build a Penrose Triangle with Legos
- How the Lego Triangle Works (Impossible triangle in Perth, Australia)
- Or Make a Paper Model
- How I Made the Image for My Playing Cards
Book Update
I’ve sent the first two Math You Can Play books to a copy editor (she edits the text part), so my focus this month is on finishing the illustrations and downloadable game boards. And designing the book covers — I think I’ll call this latest iteration done.
If everything stays on schedule, both Counting & Number Bonds and Addition & Subtraction should be available by mid- to late-spring. Fingers crossed…
Playful Math Snacks for February 2015
My February Tabletop Academy Press Updates newsletter went out this morning to everyone who signed up for math updates. If you signed up for Teresa’s fiction updates, please be patient. She writes much slower than an adult author, but we’re hoping to get her second book published in late spring.
I noticed a couple of people who joined the mailing list but neglected to ask for either the math or fantasy fiction updates — and we won’t send you any updates unless you ask for them! If you thought you signed up, but you didn’t receive this morning’s email (and it’s not in your spam folder by mistake), then leave me a comment here or just go sign up again.
If you’re not on the mailing list, you can still join in the fun:
A Preview
Math Snack: Fractal Valentines
What better way to say “I love you forever!” than with a pop-up fractal Valentine? My math club kids made these a couple years back, and they turned out great.
To make your card, choose two colors of construction paper or card stock. One color will make the pop-up hearts on the inside of your card. The other color will be the front and back of the card, and will also peek through the cut areas between the hearts. Fold the papers in half and cut them to card size.
Set the outer card aside and focus on the inside. The fractal cutting pattern is simple: press the fold, cut a curve, tuck inside, repeat…
Get in the Math Car
Get in the math car with a list of destinations and no map. Take whatever route you want, and marvel at the things you discover along the way.
— Nick Harris
CREDITS: Today’s quote is from @Mr_Harris_Math, via Twitter. Background photo courtesy of Forrest Cavale (CC0 1.0) via Unsplash.
Math Teachers at Play #82 via Mrs. E Teaches Math
The January math education blog carnival is now posted for your browsing pleasure, featuring 23 playful ways to explore mathematics from preschool to high school:
Highlights include:
Young children making bar graphs.
A wide variety of math games.
Fractions on a clothesline.
Quadrilaterals on social media.
Non-transitive dice.
Writing in math class.
Negative number calculations made physical.
Inverse trig graphing.
Function operations.
And much more!
Two Ways to Do Math
There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent.
— Raoul Bott
CREDITS: Today’s quote is from Raoul Bott, via The MacTutor History of Mathematics archive. Background photo courtesy of Swedish National Heritage Board (no known copyright restrictions) via Flickr.
Denise Gaskins' Let's Play Math 