Photo by Sister72.
Dave at MathNotations offers another version of Nim that will give your students something to think about:
[1,2]-3-[4,5]-6-[7,8]…21 Helping Children Devise and Understand Winning Strategies
Nim Revisited
How to Read a Fraction
Fraction notation and operations may be the most abstract math monsters our students meet until they get to algebra. Before we can explain those frustrating fractions, we teachers need to go back to the basics for ourselves. First, let’s get rid of two common misconceptions:
- A fraction is not two numbers.
Every fraction is a single number. A fraction can be added to other numbers (or subtracted, multiplied, etc.), and it has to obey the Distributive Law and all the other standard rules for numbers. It takes two digits (plus a bar) to write a fraction, just as it takes two digits to write the number 18 — but, like 18, the fraction is a single number that names a certain amount of whatever we are counting or measuring.
- A fraction is not something to do.
A fraction is a number, not a recipe for action. The fraction 3/4 does not mean, “Cut your pizza into 4 pieces, and then keep 3 of them.” The fraction 3/4 simply names a certain amount of stuff, more than a half but not as much as a whole thing. When our students are learning fractions, we do cut up models to help them understand, but the fractions themselves are simply numbers.
Ben Franklin Math: Elementary Problem Solving 3rd Grade
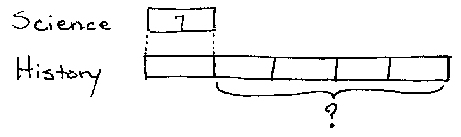
The ability to solve word problems ranks high on any math teacher’s list of goals. How can I teach my students to solve math problems? I must help them develop the ability to translate “real world” situations into mathematical language.
In two previous posts, I introduced the problem-solving tools algebra and bar diagrams. These tools help our students organize the information in a word problem and translate it into a mathematical calculation.
Working Math Problems with Poor Richard
This time I will demonstrate these problem-solving tools in action with a series of 3rd-grade problems based on the Singapore Primary Math series, level 3A. For your reading pleasure, I have translated the problems into the life of Ben Franklin, inspired by the biography Poor Richard by James Daugherty.
Continue reading Ben Franklin Math: Elementary Problem Solving 3rd Grade
Negative Numbers for Young Students
[Rescued from my old blog.]
Would you like to introduce your students to negative numbers before they study them in pre-algebra? With a whimsical number line, negative numbers are easy for children to understand.
Get a sheet of poster board, and paint a tree with roots — or a boat on the ocean, with water and fish below and bright sky above. Use big brushes and thick poster paint, so you are not tempted to put in too much detail. A thick, permanent marker works well to draw in your number line, with zero at ground (or sea) level and the negative numbers down below.
Order of Operations
[Rescued from my old blog.]
Marjorie in AZ asked a terrific question on the (now defunct) AHFH Math forum:
“…I have always been taught that the order of operations (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction) means that you work a problem in that order. All parenthesis first, then all exponents, then all multiplication from left to right, then all division from left to right, etc. …”
Many people are confused with order of operations, and it is often poorly taught. I’m afraid that Marjorie has fallen victim to a poor teacher — or at least, to a teacher who didn’t fully understand math. Rather than thinking of a strict “PEMDAS” progression, think of a series of stair steps, with the inverse operations being on the same level.
Fraction Division — A Poem
[Rescued from my old blog.]
Division of fractions is surely one of the most difficult topic in elementary arithmetic. Very few students (or teachers) actually understand how and why it works. Most of us get by with memorized rules, such as:
Ours is not to reason why;
just invert and multiply!
The Game That Is Worth 1,000 Worksheets
Have you and your children been struggling to learn the math facts? The game of Math Card War is worth more than a thousand math drill worksheets, letting you build your children’s calculating speed in a no-stress, no-test way.
Math concepts: greater-than/less-than, addition, subtraction, multiplication, division, fractions, negative numbers, absolute value, and multi-step problem solving.
Denise Gaskins' Let's Play Math 