Monday is Square Root Day

On May 5, we celebrate one of the rarest math holidays: Square Root Day, 5/5/25.

Here are a few ideas for playing math with squares and roots.

What is a Square Root?

Five is the square root of twenty-five, which means it is the number we can “square” (multiply times itself) to get 25.

The root is the base number from which the square grows. In physical terms, it is the side of the square.

Imagine a straight segment of length 5, perhaps a stick or a piece of chalk. Now lay that segment down and slide it sideways for a distance equal to its length. Drag the stick across sand, or pull the chalk across paper or a slate.

Notice how this sideways motion transforms the one-dimensional length into a two-dimensional shape, a square.

The area of this shape is the square of its root: 5 × 5 = 25.

What do you think would happen if you could drag the square through a third dimension, or drag that resulting shape through a fourth dimension?
How many shapes do you suppose might grow from that original root of 5?

Finding Squares

Gather a lot of small, square blocks like Cuisenaire rods or linking cubes. My children and I used a box of sugar cubes.

Arrange the blocks into squares of various sizes.

Notice the areas of the squares and their roots, the lengths of the sides. Talk about the patterns you see in these square numbers and their roots.

What questions can you ask?

Finding Roots

You’ve probably noticed that the square numbers are relatively rare. If you plot them on a number line or hundred chart, there’s plenty of open space between one square number and the next.

Do those “in between” numbers also have roots?

Imagine that your root-stick, instead of having length 5, was only 4 ½ units long. Could you still drag it in the sand to create a square?

What would be the area of that square?

4.5 × 4.5 = 20.25 square units.

Could you find a root that would make a square of exactly 20?

The Square Root of Two

Maybe we should start with a smaller challenge: Could you find a root that would make a square of exactly 2?

1 × 1 = 1

2 × 2 = 4

So the square root of 2 must be somewhere between 1 and 2. But where?

The answer is hiding inside the squares of one and two. Draw a two-by-two square (area = 4), and then connect the midpoints of each side to create four one-by-one squares.

Now connect the same midpoints diagonally to create a medium-size square at an angle. What is the area of that slanted square, and the length of its root?

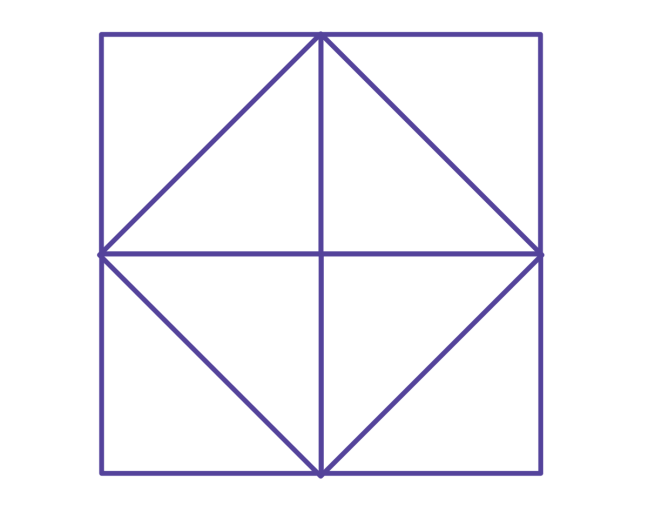
Each side of the slanted square is the diagonal of a one-by-one square. Therefore, by the Pythagorean Theorem, the side must be the square root of 2. And since it is formed by four half-squares, its area must be exactly two units.

Roots and More Roots

You can find the roots of all the whole numbers by drawing a Pythagorean Snail, which mathematicians call the “Spiral of Theodorus.”

Get a large piece of paper, a pencil, a ruler, and a drafting triangle or anything with a perfectly square corner.

Begin by drawing a line of length 1 unit near the center of your paper. This is your first root, √1.

Now use your drafting triangle to make a right angle, and draw another line of length one connected to the first. Connect the endpoints of these lines to make a triangle.

That new line is your second root, √2.

Again, make a right angle and draw another line of length one, then connect it to the previous line to create a triangle.

By the Pythagorean Theorem, this new line must be the third root, √3.

Continue drawing right triangles to create an ever-growing spiral, as shown in the image below.

Theodorus took his spiral up to √17 and proved that all of those roots were irrational numbers, except the roots of perfect squares.

If you keep going past √17, the spiral will turn around on itself, each cycle overlapping the ones before. Here is a spiral with 110 triangles.

Older Students: Look up the proof that √2 is irrational. Can you create a similar proof for √3 or any of the other non-perfect roots?

Can you show how a careless student might apply the proof to √4? Why would that proof be false?

Looking Ahead

When will be the next perfect Square Root Day? How old will you be then?

Why is there no Square Root Day next year?

Will there be a day in 2026 that we could call Square Root Approximation Day?