Children learn best through interaction with others, and mental math prompts can lead to fascinating conversations, listening as our kids apply their creativity to the many ways numbers interact.
With mental math, students master the true 3R’s of math: to Recognize and Reason about the Relationships between numbers.
And these 3Rs are the foundation of algebra, which explains why flexibility and confidence in mental math is one of the best predictors of success in high school math and beyond.
Let’s Try an Example
Multiplication involves scaling one number by another, making it grow twice as big, or three times as much, or eightfold the size. Multiplication by a fraction scales the opposite direction, shrinking to half or a third or five-ninths the original amount.
The key friendly numbers for multiplication and division are the doubles and the square numbers. As with addition and subtraction, students can estimate the answer using any math facts they know and then adjust as needed.
How many ways might children think their way through the most-missed multiplication fact, 8 × 7?
Friendly Doubles
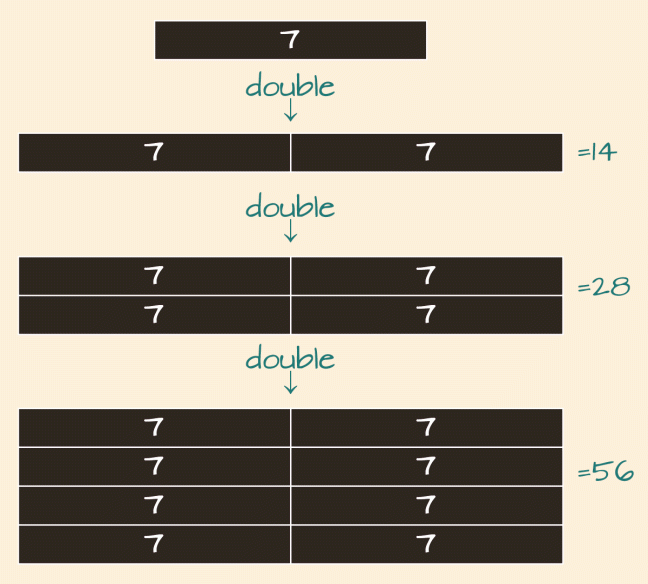
When we double a number, we get twice as much as we had at first. If we double it again, that will give us four times our original number. If we double that number a third time, then we get double-four (which is eight) times as much as the number we started with.
Times two is double, times four is double-double, and times eight is double-double-double.
So counting up eight sevens looks like this:
8 × 7 = double (double (double 7))
= double (double 14)
= double 28
= forty-sixteen
= 56
Friendly Square Numbers
Or use a square number: think of seven sevens and one more seven.
8 × 7 = (7 × 7) + 7
= 49 + 7
= 49 + 1 + 6
= 50 + 6

Another Friendly Square
Or eight eights minus one of the eights:
8 × 7 = (8 × 8) − 8
= 64 − 8
= 64 − 4 − 4
= 60 − 4
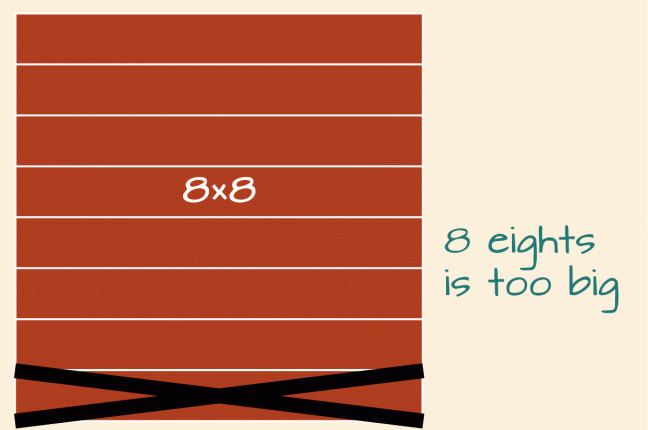
Work in Chunks
Or use the distributive property to do the calculation in smaller chunks. Think of five eights and two more eights. Two eights is a double, and five eights is easy because it’s exactly half of ten eights:
8 × 7 = (8 × 5) + (8 × 2)
= (1/2 of 80) + 16
= 40 + 16

Estimate Over and Subtract
Any number times ten is easy, and eight is almost ten. So we could find 10 sevens and then take back two of them.
8 × 7 = (10 × 7) − (2 × 7)
= 70 − 14
= 60 − 4
Can you think of another approach?
As children (and adults) play with multiplication relationships, we build skills that will help us make sense of tough topics like fractions, ratios, and proportional reasoning.
So keep practicing!
And remember, math games are a fun way to develop creative math fluency.
Read the Whole Series
Check out all the posts in my Mental Math Series:
- Mental Math Is the Key to Algebra
- Three Basic Principles
- Early Addition
- Early Subtraction
- Early Multiplication
- Coming Soon: Tips for division math facts…
* * *
Are you looking for more creative ways to play math with your kids? Check out all my books, printable activities, and cool mathy merch at Denise Gaskins’ Playful Math Store. Or join my free email newsletter.
This blog is reader-supported. If you’d like to help fund the blog on an on-going basis, then please join me on Patreon for mathy inspiration, tips, and an ever-growing archive of printable activities.
“Mental Math: Early Multiplication” copyright © 2025 by Denise Gaskins. Image at the top of the post copyright © rmarmion / Depositphotos.

Tables are there to be remembered, preferably known, not calculated each time. IMO. Most early years students I’ve met know/remember 5, 6, 7, 8. so 56 = 7 eights. Backed up by related facts: 56 / 7 = 8 and 56 / 8 = 7.
There’s no argument on our goal: Students should own the math facts and be able to use them flexibly in problem-solving.
My argument is with the method of learning. To stress memorization is to lean heavily on an unreliable foundation.
Memory is weak and easily confused. If we make memory the core of our teaching, many students will fail—usually in middle school, when the number of rules they are trying to remember has grown like a stack of Jenga blocks until everything comes crashing down.
Logic and reasoning are strong. The more we encourage children to rely on thinking their way through problems (even for math facts), the better support they have for future learning.
And then, when they’ve mastered most of the facts through regular use of logic and reasoning, it’s relatively easy to commit to memory any few stragglers.