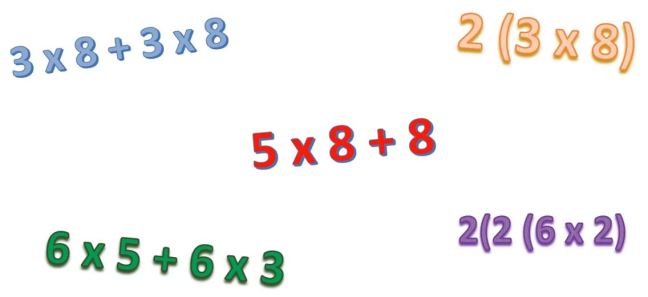Math Game Monday: Decimal Product Game

Posted on by Denise Gaskins
Learn a new math game every week, for free

This game builds understanding of decimals, and also of the inverse relationship between multiplication and division.

Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.

So what are you waiting for? Let’s play some math!

Decimal Product Game

Math Concepts: multiplying decimals, decimal place value.

Players: two players or two teams.

Equipment: printed game board, colored markers or a set of matching tokens for each player, two paperclips or other small tokens to mark the factors.

Continue reading Math Game Monday: Decimal Product Game

Math Game Monday: Math Model Rummy

Posted on by Denise Gaskins
Learn a new math game every week, for free

This game builds conceptual understanding of multiplication or fraction models.

Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.

So what are you waiting for? Let’s play some math!

Math Model Rummy

Math Concepts: multiplication or fraction models.

Players: two or more.

Equipment: one deck of math model cards, or a double deck for four or more players.

Continue reading Math Game Monday: Math Model Rummy

Math Game Monday: Tax Collector

Posted on by Denise Gaskins
Learn a new math game every week, for free

This game makes children think about multiplication and notice how prime numbers are special.

Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.

So what are you waiting for? Let’s play some math!

Tax Collector

Math Concepts: multiplication, prime numbers, factors and multiples.

Players: two or more players or two teams.

Equipment: blank paper or a printed hundred chart, pencils or markers. Calculator optional.

Continue reading Math Game Monday: Tax Collector

Math Game Monday: Scrambled Times Tables

Posted on by Denise Gaskins
Learn a new math game every week, for free

If want to drill multiplication math facts, this game is one of my favorite ways to practice.

Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.

So what are you waiting for? Let’s play some math!

Scrambled Times Tables

Math Concepts: multiplication facts, times tables.

Players: any number.

Equipment: pencil and paper, optional printed blank hundred chart.

Continue reading Math Game Monday: Scrambled Times Tables

Math Game Monday: Concentration with Math Model Cards

Posted on by Denise Gaskins
Learn a new math game every week, for free

This game lays a great foundation for your child’s understanding of multiplication and fractions.

Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.

So what are you waiting for? Let’s play some math!

Concentration with Math Model Cards

Math Concepts: multiplication or fraction models, visual/spatial memory.

Players: any number.

Equipment: one deck of math model cards.

Continue reading Math Game Monday: Concentration with Math Model Cards

Mental Math: Advanced Multiplication, Part 2

Posted on by Denise Gaskins
Father and son celebrate a mental math answer

The methods in last week’s Advanced Multiplication post only work for certain numbers, but we have another, more powerful multiplication tool: We can always use a ratio table to make sense of any multiplication.

Ratios are the beginning of proportional thinking. We can systematically alter the numbers in a ratio to reach any quantity required by our problem.

Students begin working with ratios in story problems that help them visualize and make sense of a proportional relationship.

Continue reading Mental Math: Advanced Multiplication, Part 2

Mental Math: Advanced Multiplication, Part 1

Posted on by Denise Gaskins
Mother and daughter working mental math together

Mental math is the key to algebra because the same principles underlie them both.

As our children learn to do calculations in their heads, they make sense of how numbers work together and build a strong foundation of understanding.

Remember that while mental math is always done WITH the mind, reasoning our way to the answer, it doesn’t have to be only IN the mind. Make sure your students have scratch paper or a whiteboard handy to jot down intermediate steps as needed.

Besides, math is always more fun when kids get to use colorful markers on a whiteboard.

Continue reading Mental Math: Advanced Multiplication, Part 1

Mental Math: Early Multiplication

Posted on by Denise Gaskins
mother and daughter talking math together

Children learn best through interaction with others, and mental math prompts can lead to fascinating conversations, listening as our kids apply their creativity to the many ways numbers interact.

With mental math, students master the true 3R’s of math: to Recognize and Reason about the Relationships between numbers.

And these 3Rs are the foundation of algebra, which explains why flexibility and confidence in mental math is one of the best predictors of success in high school math and beyond.

Let’s Try an Example

Multiplication involves scaling one number by another, making it grow twice as big, or three times as much, or eightfold the size. Multiplication by a fraction scales the opposite direction, shrinking to half or a third or five-ninths the original amount.

The key friendly numbers for multiplication and division are the doubles and the square numbers. As with addition and subtraction, students can estimate the answer using any math facts they know and then adjust as needed.

How many ways might children think their way through the most-missed multiplication fact, 8 × 7?

Continue reading Mental Math: Early Multiplication

If Not Methods: Multi-Digit Multiplication

Posted on by Denise Gaskins
Mother helping her daughter with math homework

As we’ve seen in earlier posts, there are more ways to solve any math problem than most people realize. Teaching children to follow memorized steps and procedures actually cripples their understanding of number relationships and patterns.

But what if our children get stumped on a multi-digit multiplication calculation like 36 × 15?

Continue reading If Not Methods: Multi-Digit Multiplication

Math Musings: Lies My Teacher Told Me

Posted on by Denise Gaskins

I mentioned last time that the common phrase “Multiplication is repeated addition” is a mathematical lie we tell our children. And it’s not the only one.

Did you ever say, “Subtraction means take-away”? Or how about “Division is sharing”? I know I have, but both of those statements are also mathematical lies.

One of the reasons I like Cuisenaire rods so much is that they can help us avoid lying to our children about math.

Continue reading Math Musings: Lies My Teacher Told Me