What we know about ancient Egyptian mathematics comes primarily from two papyri, the first one written around 1850 BC. 
This is called the Moscow papyrus, because it now belongs to Moscow’s Pushkin Museum of Fine Arts. The scroll contains 25 problems, mostly practical examples of various calculations. Problem 14, which finds the volume of a frustrum (a pyramid with its top cut off), is often cited by mathematicians as the most impressive Egyptian pyramid of all.
Trouble with Percents
Can your students solve this problem?
There are 20% more girls than boys in the senior class.
What percent of the seniors are girls?
This is from a discussion of the semantics of percent problems and why students have trouble with them, going on over at MathNotations. (Follow-up post here.)
Our pre-algebra class just finished a chapter on percents, so I thought Chickenfoot might have a chance at this one. Nope! He leapt without thought to the conclusion that 60% of the class must be girls.
After I explained the significance of the word “than”, he solved the follow-up problem just fine.
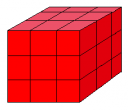
Puzzle: Random Blocks
In the first section of George Lenchner’s Creative Problem Solving in School Mathematics, right after his obligatory obeisance to George Polya (see the third quote here), Lechner poses this problem. If you have seen it before, be patient — his point was much more than simply counting blocks.
A wooden cube that measures 3 cm along each edge is painted red. The painted cube is then cut into 1-cm cubes as shown above. How many of the 1-cm cubes do not have red paint on any face?
And then he challenges us as teachers:
Do you have any ideas for extending the problem?
If so, then jot them down.
This is strategically placed at the end of a right-hand page, and I was able to resist turning to read on. I came up with a list of 15 other questions that could have been asked — some of which will be used in future Alexandria Jones stories. Lechner wrote only seven elementary-level problems, and yet his list had at least two questions that I had not considered. How many can you come up with?
Solution: The Cat’s Lasagna
The puzzle (from The mysterious temporal freeze) was:
A certain famous cat snarfs down an 11″x13″ pan of lasagna in 3 seconds flat. Assuming the fat feline has a bottomless pit for a stomach and continues to eat at the same rate, how long will it take him to devour a pasta the size of the state of Illinois?
Remember the Math Adventurer’s Rule: Figure it out for yourself! Whenever I give a problem in an Alexandria Jones story, I will try to post the answer soon afterwards. But don’t peek! If I tell you the answer, you miss out on the fun of solving the puzzle. Figure it out for yourself — and then check the answer just to prove that you got it right.
The Mysterious Temporal Freeze
Alexandria Jones stepped into the huge tent that protected her father’s excavation site from the desert winds. She laughed to herself. It was like walking into a circus.
She knelt down to whisper in the ear of her faithful dog Ramus. “In this ring, grad students carefully brush away another layer of sand. In the next ring, the artist sketches every piece as it is found.” She waved her arm. “And over there, our flashiest attraction — drum roll, please — the photographers shoot each shard of pottery from every possible angle. But where is the Master of Ceremonies?”
Alex and Rammy found Professor Jones near the back of the tent, talking to another student. While she waited for her dad, she looked through an assortment of numbered artifacts that were ready to be packed and sent to the museum.
Puzzle: Patty Paper Trisection
[Feature photo above by Michael Cory via Flickr (CC BY 2.0).]
One of the great unsolved problems of antiquity was to trisect any angle using only the basic tools of Euclidean geometry: an unmarked straight-edge and a compass. Like the alchemist’s dream of turning lead into gold, this proved to be an impossible task. If you want to trisect an angle, you have to “cheat.” A straight-edge and compass can’t do it. You have to use some sort of crutch, just as an alchemist would have to use a particle accelerator or something.
One “cheat” that works is to fold your paper. I will show you how it works, and your job is to show why.
Historical Tidbits: Alexandria Jones Answers
The Math Adventurer’s Rule: Figure It Out for Yourself!
Whenever I give a problem in an Alexandria Jones story, I will try to post the answer soon afterwards. But don’t peek! If I tell you the answer, you miss out on the fun of solving the puzzle. Figure it out for yourself — and then check the answer just to prove that you got it right.
Continue reading Historical Tidbits: Alexandria Jones Answers
Historical Tidbits: Alexandria Jones
Test Yourself: Logic
Can you solve the Wason Selection Task puzzle at Text Savvy blog? [Blog has disappeared.]
Here is an interactive version of the Wason Selection Task, and you can find out more information about it on the Wikipedia page.
Warning: Don’t read the comments Wikipedia page until you have tried the puzzle for yourself. Why ruin your fun?
Geometry: Can You Find the Center of a Circle?
For the last couple of days, I have been playing around with this geometry puzzle. If you have a student in geometry or higher math, I recommend you print out the original post (but not the comments — it’s no fun when someone gives you the answer!) and see what he or she can do with it.
[MathNotations offers many other puzzles for 7-12th grade math students. While you are at his blog, take some time to browse past articles.]
Denise Gaskins' Let's Play Math 
