[Photo by mape_s.]
I’m afraid that Math Club may have fallen victim to the economy, which is worse in our town than in the nation in general. Homeschooling families have tight budgets even in the best of times, and now they seem to be cutting back all non-essentials. I assumed that last semester’s students would return, but I should have asked for an RSVP.
Still, Kitten and I had a fun time together. We played four rounds of Tens Concentration, since I had spread out cards on the tables in the library meeting room before we realized that no one was coming. Had to pick up the cards one way or another, so we figured we might as well enjoy them! She won the first two rounds, which put her in a good mood for our lesson.
I had written “Prime numbers are like monkeys!” on the whiteboard, and Kitten asked me what that meant. That was all the encouragement I needed to launch into my planned lesson, despite the frustrating dearth of students. The idea is taken from Danica McKellar’s book Math Doesn’t Suck.
Prime Numbers . . . and Monkeys
Quoting from Ms. McKellar’s book:
Some numbers of beads cannot be evenly divided up no matter what you do. Lots of small numbers are like that: 2, 3, 5, 7. The only factors they have are 1 and themselves. There are bigger numbers like that, too, like 53 and 101. It’s hard to believe that there’s no way to evenly divide up 101, but it’s true!
I like to think of these numbers as less “evolved” than most numbers. They don’t have a whole lot going on upstairs, if you know what I mean. They’re uncomplicated. They’re “primitive,” like monkeys. (Monkeys are a type of primate.) And perhaps that is why these less-evolved numbers are called prime.
Yes, prime numbers are a bit like monkeys. Just go with me on this, okay?
Kitten is a writer, so she enjoyed the wordplay.
Factor Trees
More from Ms. McKellar:
Like monkeys swinging on the lowest branches of trees, prime numbers swing off the lowest branches of factor trees.
A factor tree is a pencil-and-paper visualization of breaking a number into its prime factors. Every number is either prime itself or it can be written as the product of two or more prime numbers.
For example:
.
.
.
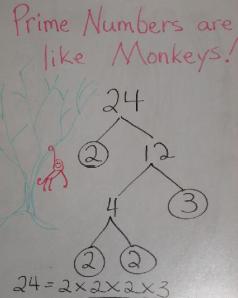
We can show this in a factor tree, where each pair of branches show two numbers that can be multiplied to make the number above them. When we find a prime factor, we circle it.
When the tree is finished, we look for all the circled numbers. Those are the prime numbers that multiply together to make the number we started with.
After I did 24 as an example, it was Kitten’s turn. She factored 84:
We noticed that if 1 was allowed to count as a prime number, the factor tree would keep branching forever and we would never get to snack time. Definitely not a good thing! No wonder mathematicians don’t count 1 among the primes.
Then we worked together to factor 700,700. Kitten finished up the lesson by figuring out that today is January ,
.
Kitten’s Conclusion
With no other kids around (and Mom trying to stick to her diet), Kitten got first dibs on the snacks. We finished up the last two games of Concentration, then cleaned the meeting room and stacked all the chairs.
On the way home from the library, Kitten said, “I like Prime Monkeys. They’re fun!”
From a child who once wrote “I hate hate hate hate hate hate math!” all over the back of her Miquon workbook, that is high praise, indeed.


Don’t worry! We, your blog readers, are your students! And we don’t even need a snack.
Love the prime monkeys. That’s the kind of thing that sticks in your head.
Thanks!
Valerie
I agree with Valerie on all counts. First, your readers are still here. I just found your blog and it got my interest. And I’ll just state for the record that math is not my subject. Every once in a while I find somebody who can make me appreciate math, but I still wouldn’t jump to loving it. (I do algebra on sticky notes in my down time, but don’t tell anybody lol.)
Sorry your students dwindled down, but maybe once things pick back up your students can return. Unfortunately I don’t think parents realize that it’s during this stage when it’s really a great idea to be able to keep things like this in children’s lives even if it does seem non-essential in the grand scheme of things, it’s essential for them.
Best wishes.
Thanks for the encouragement! (Although unfortunately, blog readers don’t pay the bills.)
On the way home, as we chatted a bit about the lesson, we decided the prime monkeys would have been even more memorable if we had our normal group of energetic boys there. The math club girls are pretty quiet, but I can imagine the boys adding sound effects and scratch-under-the-arms motions to each factor tree:
“There’s another prime. Hoo-oo-oo!”
Nice thing, though mathematically speaking it’s a bit demeaning for the importance of prime numbers. With relation to their being the fundamental factors of all other [composite] numbers, you could’ve explained how they’re more “important”, hence prime, than calling them primate! It hurts! Funnily, nevertheless! Awesome incident though. Reached here with regard to your e-day post. Happy belated e-day! 🙂
You are right — that is what “prime” really means. But Ms. McKellar’s wordplay with the monkeys is so memorable, especially for a middle school student, that I don’t know if I could bring myself to teach this any other way.
We have been working with fractions, and Kitten finds herself using prime monkeys nearly every day. Here’s hoping she grows to understand the prime importance of these numbers through continued use!
oh wow, I loved, loved, loved this! Can’t wait to dive into monkeys with my kids!
This sounds like an interesting book! Thank you for sharing about the prime numbers and monkeys!
Well, thank you for the math snack! Mouse was struggling with prime numbers the other day. Maybe I’ll show her this and see if it helps. 🙂
I should point out that this came after several lessons about prime numbers in general. I usually start teaching primes with blocks or other small manipulatives that can be arranged into rectangular arrays.
With a given number of blocks, how many different arrays can you make?
The sides of each rectangle (the number of rows and columns) are factors of the number. Prime numbers are those which can only make long, skinny 1x__ arrays. Composite numbers can make two or more different rectangles. Sometimes we shift to graph paper to see if we can color all the rectangles for each number from 1 to 50 (or 100, depending on the time available and the student’s patience).
Oh wow. I’ve been teaching Geometry for four years, during the course of which I teach prime factorization for the purposes of simplifying radicals. I’ve NEVER thought of the analogy of prime numbers being like monkeys but it is hilarious! I’m going to use it next year to spice up my lessons! Thanks…
I can’t take credit for the analogy; it’s from Danica McKellar’s book. She uses wordplay and other mnemonics to help students remember the math tips and tricks.
Hello! We, Marta and Monica, are studying to become math teachers and computation at Catholic University of Maule, Chile.
Our english teacher gae us the asignment to look up in the internet for a math blog, that’s when we found your blog and it caught our attention. It’s not usual for us for student to be homeschooled, almost every children here goes to school. We like the way you teach math because you try to bring children and math together using analogies with things they may like or find more interesting. (Like comparing Prime numbers with monkeys)
We think we might use it when it’s our turn to teach actual students.
Keep up the good work! We’ll be cheking up your blog very often.
Cheers from Chile,
Monica and Marta.
I’m glad you enjoyed my blog. Best wishes on your studies!
Virtual snacks please?
I’ve heard the internet explorer has these things called *cookies* but I could never find them on mine. 😦 Me want cookie!
I agree, Kyle. If this blog is a virtual math club, we should definitely have virtual snacks! How about these cookies?
Me and Prime Numbers do not mix.
Hi Denise
Thank you so much for being into prime numbers. As far as primates go, this just flew into my head today: The (sum of the) first prime is 2, for our two hands. The sum of the first two primes is 5 (2 + 3), for the fingers on one hand. The sum of the first three primes is 10 (2 + 3 + 5), for all of the fingers (my apologies to those with less, or more than five fingers on each hand). The sum of the first four primes is 17. 17 is wonderful and popular, but I don’t know more than that along these lines.
That is a small tidbit, but it makes me that much happier to be a primate…