Almost all math problems call for the student to assume one thing or another. Without assumptions — definitions, postulates, axioms, common notions, or whatever you want to call them — mathematics of any kind is impossible. Tony at Pencils Down (who plans to be a math teacher when he grows up) reminds us that, necessary though it may be, we are stepping on dangerous ground when we assume:
Blog
Math Carnival #18
Carnival of Math #18 was posted Saturday evening at JD2718. Jonathan has put together a tremendous list of 52 blog posts, with these instructions:
1) Scroll, 2) Click, 3) Enjoy, 4) Repeat.
It is too much to take in on a sleepy Sunday afternoon, but I know I have some great math reading to look forward to this week.
Edited to add: There is an addendum post, too. Enjoy!
Quotations XVI: Back to the Blackboard
Classes are back in session at our homeschool co-op, so I am again collecting short quotes for the blackboard. Here are the ones I used in September:
Any fool can know. The point is to understand.
Life without geometry is pointless.
You don’t understand anything until you learn it more than one way.
Blog Carnivals = Browsing Pleasure
92nd Carnival of Homeschooling
Charlotte Mason Carnival: Music/Composer Study
And the Homeschool Blog Awards site is gearing up for this year’s program, for anyone who reads homeschooling blogs — and that’s all of us, right?
Ben Franklin Math: Elementary Problem Solving 3rd Grade
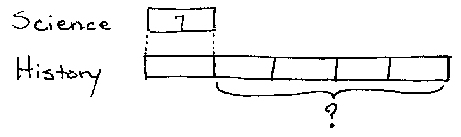
The ability to solve word problems ranks high on any math teacher’s list of goals. How can I teach my students to solve math problems? I must help them develop the ability to translate “real world” situations into mathematical language.
In two previous posts, I introduced the problem-solving tools algebra and bar diagrams. These tools help our students organize the information in a word problem and translate it into a mathematical calculation.
Working Math Problems with Poor Richard
This time I will demonstrate these problem-solving tools in action with a series of 3rd-grade problems based on the Singapore Primary Math series, level 3A. For your reading pleasure, I have translated the problems into the life of Ben Franklin, inspired by the biography Poor Richard by James Daugherty.
Continue reading Ben Franklin Math: Elementary Problem Solving 3rd Grade
Play This Anti-Phishing Game
Do your students know how to protect themselves from email scams? Can they recognize fraudulent websites? Can you? Test your online security savvy by playing this educational game from Carnegie Mellon University:
Carnival, Carnival, Carnival
The Carnival of Education: Week 137…er, 138?
Charlotte Mason Blog Carnival – First Edition
And what goes together better than homeschooling, families, and frugal living?
While I Was Distracted…
After a hectic couple of weeks, I finally found a little time to sit at the computer and browse — and boy, was I amazed to see what I had missed! If you have not yet read Dave‘s interview with Prof. Lynn Arthur Steen about the state of math education reform, click over and check it out: Part I here, and Part II here.
According to the intro, Prof. Steen “has been a driving force for the reform of school mathematics for many years and was on the development team that produced NCTM’s Curriculum and Evaluation Standards for School Mathematics. For the last few years, he has been involved in Achieve’s commitment to developing world-class mathematics standards for K-8 and ADP’s similar commitment to secondary mathematics.” He has some interesting things to say, although many of his statements are open to various interpretations, and at times he seems determined to provoke a hot-headed response. For instance:
Carnival of Mathematics Growing Up
Dave at MathNotations was up early today posting the 17th Edition of the Carnival of Mathematics. 17 is sometimes called the most “random” number, although one (not very scientific) test has shown 3 to be even more “random.”
Did you know there are only 17 ways you can design wallpaper? The 17 Wallpaper Tilings has animations of each pattern.
Reading to Learn Math
[Photo by Betsssssy.]
Do you ever take your kids’ math tests? It helps me remember what it is like to be a student. I push myself to work quickly, trying to finish in about 1/3 the allotted time, to mimic the pressure students feel. And whenever I do this, I find myself prone to the same stupid mistakes that students make.
Even teachers are human.
In this case, it was a multi-step word problem, a barrage of information to stumble through. In the middle of it all sat this statement:
…and there were 3/4 as many dragons as gryphons…
My eyes saw the words, but my mind heard it this way:
…and 3/4 of them were dragons…
What do you think — did I get the answer right? Of course not! Every little word in a math problem is important, and misreading even the smallest word can lead a student astray. My mental glitch encompassed several words, and my final tally of mythological creatures was correspondingly screwy.
But here is the more important question: Can you explain the difference between these two statements?
Denise Gaskins' Let's Play Math 