What Do You Notice? What Do You Wonder?

Posted on by Denise Gaskins

Drawing Star

If you want your children to understand and enjoy math, you need to let them play around with beautiful things and encourage them to ask questions.

Here is a simple yet beautiful thing I stumbled across online today, which your children may enjoy:

It reminds me of string art designs, but the app makes it easy to vary the pattern and see what happens.

  • What do your students notice about the patterns?
  • What questions can they ask?

I liked the way the app uses “minutes” as the unit that describes the star you want the program to draw. That makes it easier (for me, at least) to notice and understand the patterns, since minutes are a more familiar and intuitive unit than degrees, let alone radians.

Continue reading What Do You Notice? What Do You Wonder?

Math Teachers at Play #62: A Carnival with Books

Posted on by Denise Gaskins

by Robert Webb

Do you enjoy math? I hope so! If not, browsing this post just may change your mind. Welcome to the Math Teachers At Play blog carnival — a smorgasbord of ideas for learning, teaching, and playing around with math from preschool to pre-college.

Let the mathematical fun begin!

POLYHEDRON PUZZLE

By tradition, we start the carnival with a puzzle in honor of our 62nd edition:

An Archimedean solid is a polyhedron made of two or more types of regular polygons meeting in identical vertices. A rhombicosidodecahedron (see image above) has 62 sides: triangles, squares, and pentagons.

  • How many of each shape does it take to make a rhombicosidodecahedron?
Click for full-size template.
Click for template.

My math club students had fun with a Polyhedra Construction Kit. Here’s how to make your own:

  1. Collect a bunch of empty cereal boxes. Cut the boxes open to make big sheets of cardboard.
  2. Print out the template page (→) and laminate. Cut out each polygon shape, being sure to include the tabs on the sides.
  3. Turn your cardboard brown-side-up and trace around the templates, making several copies of each polygon. I recommend 20 each of the pentagon and hexagon, 40 each of the triangle and square.
  4. Draw the dark outline of each polygon with a ballpoint pen, pressing hard to score the cardboard so the tabs will bend easily.
  5. Cut out the shapes, being careful around the tabs.
  6. Use small rubber bands to connect the tabs. Each rubber band will hold two tabs together, forming one edge of a polyhedron.

So, for instance, it takes six squares and twelve rubber bands to make a cube. How many different polyhedra (plural of polyhedron) will you make?

  • Can you build a rhombicosidodecahedron?

And now, on to the main attraction: the 62 blog posts. Many of the following articles were submitted by their authors; others were drawn from the immense backlog in my blog reader. If you’d like to skip directly to your area of interest, here’s a quick Table of Contents:

Continue reading Math Teachers at Play #62: A Carnival with Books

Homeschooling High School Math

Posted on by Denise Gaskins
photo by ddluong via flickr
photo by ddluong via flickr

Feature photo (above) by Sphinx The Geek via flickr.

Most homeschoolers feel at least a small tinge of panic as their students approach high school. “What have we gotten ourselves into?” we wonder. “Can we really do this?” Here are a few tips to make the transition easier.

Before you move forward, it may help to take a look back. How has homeschooling worked for you and your children so far?

If your students hate math, they probably never got a good taste of the “Aha!” factor, that Eureka! thrill of solving a challenging puzzle. The early teen years may be your last chance to convince them that math can be fun, so consider putting aside your textbooks for a few months to:

On the other hand, if you have delayed formal arithmetic, using your children’s elementary years to explore a wide variety of mathematical adventures, now is a good time to take stock of what these experiences have taught your students.

  • How much of what society considers “the basics” have your children picked up along the way?
  • Are there any gaps in their understanding of arithmetic, any concepts you want to add to their mental tool box?

Continue reading Homeschooling High School Math

Math Teachers at Play #58: Crazy, Funny Math

Posted on by Denise Gaskins

No 58 - gold on blue[Feature photo (above) by Alex Kehr. Photo (right) by kirstyhall via flickr.]

Welcome to the Math Teachers At Play blog carnival — a smorgasbord of ideas for learning, teaching, and playing around with math from preschool to pre-college. If you like to learn new things and play around with ideas, you are sure to find something of interest.

Let the mathematical fun begin…

PUZZLE 1

By tradition, we start the carnival with a pair of puzzles in honor of our 58th edition. Click to download the pdf:

How CRAZY Can You Make It

Continue reading Math Teachers at Play #58: Crazy, Funny Math

What Is a Proof?

Posted on by Denise Gaskins

I’ve been enjoying the Introduction to Mathematical Thinking course by Keith Devlin. For the first few weeks, we mostly talked about language, especially the language of logical thinking. This week, we started working on proofs.

For a bit of fun, the professor emailed a link to this video. My daughter Kitten enjoyed it, and I hope you do, too.

Full lesson available at Ted-Ed.

Who Killed Professor X?

Posted on by Denise Gaskins

What a Fun Book!

professorX

Who Killed Professor X? is a work of fiction based on actual incidents, and its heroes are real people who left their mark on the history of mathematics. The murder takes place in Paris in 1900, and the suspects are the greatest mathematicians of all time. Each suspect’s statement to the police leads to a mathematical problem, the solution of which requires some knowledge of secondary-school mathematics. But you don’t have to solve the puzzles in order to enjoy the book.

Fourteen pages of endnote biographies explain which parts of the mystery are true, which details are fictional, and which are both (true incidents slightly modified for the sake of the story).

My daughter Kitten, voracious as always, devoured it in one sitting — and even though she hasn’t studied high school geometry yet, she was able to work a couple of the problems.

Lockhart’s Measurement

Posted on by Denise Gaskins

After watching the video on the Amazon.com page, this book has jumped to the top of my wish list.

You may have read Paul Lockhart’s earlier piece, A Mathematician’s Lament, which explored the ways that traditional schooling distorts mathematics. In this book, he attempts to share the wonder and beauty of math in a way that anyone can understand.

According to the publisher: “Measurement offers a permanent solution to math phobia by introducing us to mathematics as an artful way of thinking and living. Favoring plain English and pictures over jargon and formulas, Lockhart succeeds in making complex ideas about the mathematics of shape and motion intuitive and graspable.”

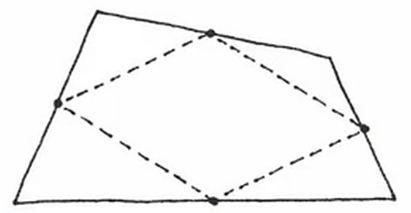
If you take any 4-sided shape at all — make it as awkward and as ridiculous as you want — if you take the middles of the sides and connect them, it always makes a parallelogram. Always! No matter what crazy, kooky thing you started with.

That’s scary to me. That’s a conspiracy.

That’s amazing!

That’s completely unexpected. I would have expected: You make some crazy blob and connect the middles, it’s gonna be another crazy blob. But it isn’t — it’s always a slanted box, beautifully parallel.

WHY is it that?!

The mathematical question is “Why?” It’s always why. And the only way we know how to answer such questions is to come up, from scratch, with these narrative arguments that explain it.

So what I want to do with this book is open up this world of mathematical reality, the creatures that we build there, the questions that we ask there, the ways in which we poke and prod (known as problems), and how we can possibly craft these elegant reason-poems.

— Paul Lockhart
author of Measurement