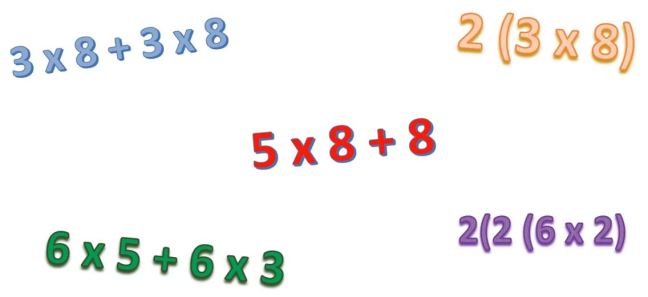Mental Math: Early Division

Posted on by Denise Gaskins
Boy doing mental math calculation

Mental math is doing calculations with our minds, though we can use scratch paper or whiteboards to make notes as we work.

Doing mental math, children use the basic principles of arithmetic to simplify problems so they can think about number relationships, mastering the basic structures of how numbers work, the same structures that underlie algebraic reasoning.

As always, we rely on two key mental-math strategies.

  • Use friendly numbers.
  • Estimate, then adjust.

Division is the mirror image of multiplication, the inverse operation that undoes multiplication, which means we are scaling numbers down into smaller parts. Important friendly numbers include halves, thirds, and tenths, plus the square numbers and any multiplication facts the student happens to remember.

Continue reading Mental Math: Early Division

Mental Math: Early Multiplication

Posted on by Denise Gaskins
mother and daughter talking math together

Children learn best through interaction with others, and mental math prompts can lead to fascinating conversations, listening as our kids apply their creativity to the many ways numbers interact.

With mental math, students master the true 3R’s of math: to Recognize and Reason about the Relationships between numbers.

And these 3Rs are the foundation of algebra, which explains why flexibility and confidence in mental math is one of the best predictors of success in high school math and beyond.

Let’s Try an Example

Multiplication involves scaling one number by another, making it grow twice as big, or three times as much, or eightfold the size. Multiplication by a fraction scales the opposite direction, shrinking to half or a third or five-ninths the original amount.

The key friendly numbers for multiplication and division are the doubles and the square numbers. As with addition and subtraction, students can estimate the answer using any math facts they know and then adjust as needed.

How many ways might children think their way through the most-missed multiplication fact, 8 × 7?

Continue reading Mental Math: Early Multiplication

Mental Math: Early Subtraction

Posted on by Denise Gaskins
mother and child doing math homework

By doing mental math, we help our children use the basic principles of arithmetic to simplify problems so they can think about number relationships, mastering the basic structures of how numbers work.

And the more our children practice these structures in mental math, the better prepared they will be to recognize the same principles in algebra.

The basic idea of subtraction is finding the difference between two quantities: comparing a larger amount to a smaller one, figuring out what’s left when you remove a part, or finding the distance between two measurements (or two points on the number line).

When you work with young children learning subtraction, remember our two key mental-math strategies.

  • Use friendly numbers.

For early subtraction with numbers less than 20, the most important friendly numbers are 5 and 10, the pairs of numbers that make 10, and the doubles.

  • Estimate, then adjust.

When children apply their creative minds to reasoning about math, they can use friendly numbers to get close to an answer, and then tweak the result as needed.

Continue reading Mental Math: Early Subtraction

Mental Math: Early Addition

Posted on by Denise Gaskins
child counting on fingers

From the very beginning of a child’s experience with math, we want to focus on reasoning, making sense of numbers, thinking about how they relate to each other and how we can use these relationships to solve problems.

The basic idea of addition is putting like things together: combining parts to make a whole thing, putting together sets to make a collection, or starting with an original amount and adding the increase as it grows. Connecting two numbers in relationship with a third number we call the sum.

When you work with young children learning addition, remember the two key mental-math strategies I mentioned in the previous post.

  • Use friendly numbers.

For early single-digit addition, the most important friendly numbers are 5 and 10, the pairs of numbers that make 10, and the doubles.

  • Estimate, then adjust.

When children apply their creative minds to reasoning about math, they can use friendly numbers to get close to an answer, and then tweak the result as needed.

Continue reading Mental Math: Early Addition

FAQ: The Necessity of Math Facts

Posted on by Denise Gaskins

Ah, math facts — the topic that just won’t stop giving grief to students and anxiety to their parents. So it happened that I got another question, but this one leaned in a more philosophical direction…

“I enjoyed your podcast interview on Cultivating Math Curiosity and Reasoning in Kids. I love the idea that we don’t have to make our children memorize everything in math. We can give them freedom to make mental connections for themselves.

    “But on the other hand, we don’t have unlimited time for them to figure things out on their own, do we? What about children who can’t make these connections for themselves?

      “For example, what about the math facts? If my kids aren’t picking them up, don’t they just have to memorize them?”

      Continue reading FAQ: The Necessity of Math Facts

      FAQ: Memorizing the Math Facts

      Posted on by Denise Gaskins

      It came up again this week, one of the most frequently asked questions about homeschooling math:

      “I believe it’s important for children to memorize the math facts, but my kids are struggling with mental math. How can I help them master these important number relationships?”

      We all want our children to own the math facts, those basic relationships between small numbers that form the foundation of all arithmetic.

      But I don’t think emphasizing memorization will develop the sort of fluency your children need.

      The human brain remembers what it thinks about, so we want children using their brains and thinking as deeply as possible about number relationships from as many different perspectives as we can get, noticing patterns, finding connections, making sense of the math.

      Continue reading FAQ: Memorizing the Math Facts

      Only Three Facts to Memorize

      Posted on by Denise Gaskins

      A comment from a friend got me playing around with multiplication. I found a few videos from some of my favorite math people, so I’ll be sharing over the next few days.

      Here’s one from Sonya Post of Learning Well at Home. Also, Sonya just hosted Playful Math Education Carnival #143, which is well worth your time to explore!

      https://youtu.be/zQkWmsCCvNk7rel=0

      Did your device hide the video? Find it on YouTube here.

      “When students have to drill multiplication facts, it’s frustrating, unproductive and it makes them hate math. A better way to master the multiplication table is work on the skills that allow students to multiply quickly and efficiently.”

      —Sonya Post, Why We Don’t Drill Multiplication Facts – What We Do Instead

      Doubling and Halving

      Making doubles and halves are a great foundation for all sorts of math.

      Do you ever play the doubling game with your children? One player picks a starting number, and then you take turns doubling it until your mental math skills run out. How far can you go?

      Or try the halving game: One player chooses a starting number, and you take turns cutting it in half. How tiny can you go?

      As Sonya demonstrated, these skills help your child master their multiplication facts. And they are fantastic preparation for exponents and logarithms, too!

      Memorizing the Math Facts

      Posted on by Denise Gaskins

      Central City Times Tables[Photo by dsb nola via flickr. (CC BY 2.0)]

      The most effective and powerful way I’ve found to commit math facts to memory is to try to understand why they’re true in as many ways as possible. It’s a very slow process, but the fact becomes permanently lodged, and I usually learn a lot of surrounding information as well that helps me use it more effectively.
      …
      Actually, a close friend of mine describes this same experience: he couldn’t learn his times tables in elementary school and used to think he was dumb. Meanwhile, he was forced to rely on actually thinking about number relationships and properties of operations in order to do his schoolwork. (E.g. I can’t remember 9×5, but I know 8×5 is half of 8×10, which is 80, so 8×5 must be 40, and 9×5 is one more 5, so 45. This is how he got through school.) Later, he figured out that all this hard work had actually given him a leg up because he understood numbers better than other folks. He majored in math in college and is now a cancer researcher who deals with a lot of statistics.

      — Ben Blum-Smith
      Comment on Math Mama’s post What must be memorized?

      The entire discussion (article and comments) is well worth reading:

      You may also enjoy:

      Quotable: Learning the Math Facts

      Posted on by Denise Gaskins

      Feature photo above by USAG- Humphreys via Flickr (CC BY 2.0).

      During off-times, at a long stoplight or in grocery store line, when the kids are restless and ready to argue for the sake of argument, I invite them to play the numbers game.

      “Can you tell me how to get to twelve?”

      My five year old begins, “You could take two fives and add a two.”

      “Take sixty and divide it into five parts,” my nearly-seven year old says.

      “You could do two tens and then take away a five and a three,” my younger son adds.

      Eventually we run out of options and they begin naming numbers. It’s a simple game that builds up computational fluency, flexible thinking and number sense. I never say, “Can you tell me the transitive properties of numbers?” However, they are understanding that they can play with numbers.

      …

      photo by Mike Baird via flickr
      photo by Mike Baird via flickr

      I didn’t learn the rules of baseball by filling out a packet on baseball facts. Nobody held out a flash card where, in isolation, I recited someone else’s definition of the Infield Fly Rule. I didn’t memorize the rules of balls, strikes, and how to get someone out through a catechism of recitation.

      Instead, I played baseball.

      — John Spencer
      Memorizing Math Facts

      Conversational Math

      The best way for children to build mathematical fluency is through conversation. For more ideas on discussion-based math, check out these posts:

      Learning the Math Facts

      For more help with learning and practicing the basic arithmetic facts, try these tips and math games:

       
      * * *

      This blog is reader-supported.

      If you’d like to help fund the blog on an on-going basis, then please join me on Patreon for mathy inspiration, tips, and an ever-growing archive of printable activities.

      If you liked this post, and want to show your one-time appreciation, the place to do that is PayPal: paypal.me/DeniseGaskinsMath. If you go that route, please include your email address in the notes section, so I can say thank you.

      Which I am going to say right now. Thank you!

      “Quotable: Learning the Math Facts” copyright © 2013 by Denise Gaskins. Image at the top of the post copyright © USAG- Humphreys via Flickr (CC BY 2.0).

      How to Conquer the Times Table, Part 5

      Posted on by Denise Gaskins

      Photo of Lex times 11, by Dan DeChiaro, via flickr.

      We are finishing up an experiment in mental math, using the world’s oldest interactive game — conversation — to explore multiplication patterns while memorizing as little as possible.

      Take your time to fix each of these patterns in mind. Ask questions of your student, and let her quiz you, too. Discuss a variety of ways to find each answer. Use the card game Once Through the Deck (explained in part 3)as a quick method to test your memory. When you feel comfortable with each number pattern, when you are able to apply it to most of the numbers you and your child can think of, then mark off that row and column on your times table chart.

      So far, we have studied the times-1 and times-10 families and the Commutative Property (that you can multiply numbers in any order). Then we memorized the doubles and mastered the facts built on them. And then last time we worked on the square numbers and their next-door neighbors.

      Continue reading How to Conquer the Times Table, Part 5