Since I’ve been posting new Alexandria Jones stories this week (beginning here), I’ve gone back and re-read the old Christmas posts. I noticed that the original Graph-It Game included a religious design, but nothing for those who don’t celebrate Christmas.
So I updated the post with a new, non-religious puzzle. Here it is, if you want to play…
Graph-It Game Design
For this design, you will need graph paper with coordinates from −8 to +8 on both the x- and y-axis. Connect the points in each line. Stop at the periods, and then start a new line at the next point.
(-8,8) – (-8,0) – (0,8) – (-8,8) – (-4,4) – (0,4) – (0,8) – (8,8) – (4,4) – (0,8).
(8,8) – (8,0) – (4,0) – (4,-4) – (8,0) – (8,-8) – (0,-8) – (4,-4) – (0,-4) – (0,-8) – (-8,0) – (-8, -8) – (0,-8).
(-8,-8) – (4,4) – (0,4) – (4,0) – (4,4) – (8,0).
(8,-8) – (-4,4) – (-4,-4) – (0,-4) – (-4,0) – (-8,0).
(0,-2) – (0,-4) – (4,0) – (2,0) – (2,-2) – (-2,-2) – (-2,2) – (2,2) – (2,0) – (1,1) – (1,0) – (2,0) – (0,-2) – (-2,0) – (0,2) – (1,1) – (-1,1) – (-1,-1) – (1,-1) – (1,0) – (-4,0) – (0,4) – (0,-1) – (-1,0) – (0,1) – (1,0) – (0,-1) – (0,-2).
Color in your design and hang it up for the whole family to enjoy!
Now Make Your Own
Of course, the fun of the Graph-It Game is to make up your own graphing puzzle. Can you create a coordinate design for your friends to draw?
Want More?
You can see all the Alexandria Jones Christmas posts at a glance here:
CREDITS: “Love Christmas Lights” photo by Kristen Brasil via Flickr (CC BY 2.0).


 Are all numbers polite?
Are all numbers polite? 






 I’d love to hear your favorite math explorations or journaling tips!
I’d love to hear your favorite math explorations or journaling tips! 



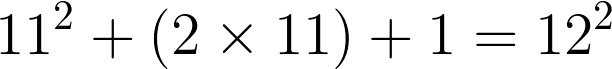
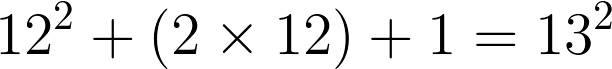


 People assume that because I teach math, blog about math, give advice about math on internet forums, and present workshops about teaching math — because I do all this, I must be good at math.
People assume that because I teach math, blog about math, give advice about math on internet forums, and present workshops about teaching math — because I do all this, I must be good at math. 





