While I was working on the next post in my PUFM Series, I stumbled on an old favorite video. Since I couldn’t think of an excuse to use it in a post about multiplication, I decided to share it today. Enjoy!
Problem-Solving Poll: What’s Your Answer?
[Photo by Alex E. Proimos via flickr.]
Patrick Vennebush, author of Math Jokes 4 Mathy Folks (the book and the blog) wants to know how you and your children would answer a tricky math problem.
I have often heard that, “Good teachers borrow, great teachers steal.” So today, I am stealing one of Marilyn Burns’s most famous problems. She takes this problem to the streets, and various adults give lots of different answers. When I’ve used it in workshops, even among a mathy crowd, I get lots of different answers, too.
What’s your answer?
“A man buys a truck for $600, then sells it for $700. Later, he decides to buy it back again and pays $800 dollars. However…”
Update: Patrick posted the solution and percentages correct for students of various ages.
Lockhart’s Measurement
After watching the video on the Amazon.com page, this book has jumped to the top of my wish list.
You may have read Paul Lockhart’s earlier piece, A Mathematician’s Lament, which explored the ways that traditional schooling distorts mathematics. In this book, he attempts to share the wonder and beauty of math in a way that anyone can understand.
According to the publisher: “Measurement offers a permanent solution to math phobia by introducing us to mathematics as an artful way of thinking and living. Favoring plain English and pictures over jargon and formulas, Lockhart succeeds in making complex ideas about the mathematics of shape and motion intuitive and graspable.”
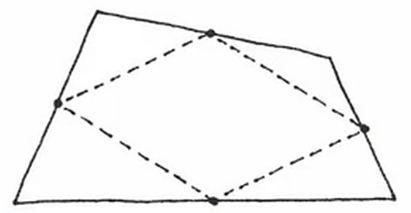
If you take any 4-sided shape at all — make it as awkward and as ridiculous as you want — if you take the middles of the sides and connect them, it always makes a parallelogram. Always! No matter what crazy, kooky thing you started with.
That’s scary to me. That’s a conspiracy.
That’s amazing!
That’s completely unexpected. I would have expected: You make some crazy blob and connect the middles, it’s gonna be another crazy blob. But it isn’t — it’s always a slanted box, beautifully parallel.
WHY is it that?!
The mathematical question is “Why?” It’s always why. And the only way we know how to answer such questions is to come up, from scratch, with these narrative arguments that explain it.
So what I want to do with this book is open up this world of mathematical reality, the creatures that we build there, the questions that we ask there, the ways in which we poke and prod (known as problems), and how we can possibly craft these elegant reason-poems.
— Paul Lockhart
author of Measurement
Rate × Time = Distance Problems
I love how Richard Rusczyk explains math problems. It’s a new school year, and that means it’s time for new MathCounts Mini videos. Woohoo!
- Download the activity sheet with warm-up and follow-up problems.
Build Mathematical Skills by Delaying Arithmetic, Part 4
To my fellow homeschoolers,
While Benezet originally sought to build his students’ reasoning powers by delaying formal arithmetic until seventh grade, pressure from “the deeply rooted prejudices of the educated portion of our citizens” forced a compromise. Students began to learn the traditional methods of arithmetic in sixth grade, but still the teachers focused as much as possible on mental math and the development of thinking strategies.
Notice how waiting until the children were developmentally ready made the work more efficient. Benezet’s students studied arithmetic for only 20-30 minutes per day. In a similar modern-day experiment, Daniel Greenberg of Sudbury School discovered the same thing: Students who are ready to learn can master arithmetic quickly!
Grade VI
[20 to 25 minutes a day]
At this grade formal work in arithmetic begins. Strayer-Upton Arithmetic, book III, is used as a basis.
[Note: Essentials of Arithmetic by George Wentworth and David Eugene Smith is available free and would probably work as a substitute.]
The processes of addition, subtraction, multiplication, and division are taught.
Care is taken to avoid purely mechanical drill. Children are made to understand the reason for the processes which they use. This is especially true in the case of subtraction.
Problems involving long numbers which would confuse them are avoided. Accuracy is insisted upon from the outset at the expense of speed or the covering of ground, and where possible the processes are mental rather than written.
Before starting on a problem in any one of these four fundamental processes, the children are asked to estimate or guess about what the answer will be and they check their final result by this preliminary figure. The teacher is careful not to let the teaching of arithmetic degenerate into mechanical manipulation without thought.
Fractions and mixed numbers are taught in this grade. Again care is taken not to confuse the thought of the children by giving them problems which are too involved and complicated.
Multiplication tables and tables of denominate numbers, hitherto learned, are reviewed.
— L. P. Benezet
The Teaching of Arithmetic II: The Story of an experiment
Continue reading Build Mathematical Skills by Delaying Arithmetic, Part 4
Build Mathematical Skills by Delaying Arithmetic, Part 3
To my fellow homeschoolers,
How can our children learn mathematics if we delay teaching formal arithmetic rules? Ask your librarian to help you find some of the wonderful living books about math. Math picture books are great for elementary students. Check your library for the Time-Life “I Love Math” books or the “Young Math Book” series. You’ll be amazed at the advanced topics your children can understand!
Benezet’s students explored their world through measurement, estimation, and mental math. Check out my PUFM Series for mental math thinking strategies that build your child’s understanding of number patterns and relationships.
Grade IV
Still there is no formal instruction in arithmetic.
By means of foot rules and yard sticks, the children are taught the meaning of inch, foot, and yard. They are given much practise in estimating the lengths of various objects in inches, feet, or yards. Each member of the class, for example, is asked to set down on paper his estimate of the height of a certain child, or the width of a window, or the length of the room, and then these estimates are checked by actual measurement.
The children are taught to read the thermometer and are given the significance of 32 degrees, 98.6 degrees, and 212 degrees.
They are introduced to the terms “square inch,” “square foot,” and “square yard” as units of surface measure.
With toy money [or real coins, if available] they are given some practise in making change, in denominations of 5’s only.
All of this work is done mentally. Any problem in making change which cannot be solved without putting figures on paper or on the blackboard is too difficult and is deferred until the children are older.
Toward the end of the year the children will have done a great deal of work in estimating areas, distances, etc., and in checking their estimates by subsequent measuring. The terms “half mile,” “quarter mile,” and “mile” are taught and the children are given an idea of how far these different distances are by actual comparisons or distances measured by automobile speedometer.
The table of time, involving seconds, minutes, and days, is taught before the end of the year. Relation of pounds and ounces is also taught.
— L. P. Benezet
The Teaching of Arithmetic II: The Story of an experiment
Continue reading Build Mathematical Skills by Delaying Arithmetic, Part 3
Cool Fibonacci Conversion Trick

Maria explains how to use the Fibonacci Numbers to convert distance measurements between miles and kilometers:
P.S.: Congratulations to Maria for her Math Mammoth program being featured in the latest edition of Cathy Duffy’s 100 Top Picks for Homeschool Curriculum! And Home School Buyer’s Co-op has a sale on Cathy Duffy’s book through the end of July.
Sample The Moscow Puzzles
Dover Publications is offering a free sample chapter from The Moscow Puzzles.
Cat and Mice
Purrer has decided to take a nap. He dreams he is encircle by 13 mice: 12 gray and 1 white. He hears his owner saying: “Purrer, you are to eat each thirteenth mouse, keeping the same direction. The last mouse you eat must be the white one.”
More Free Math from Dover Publications
Olympic Logic
I love logic puzzles! Nrich Maths offers four fun Olympics Logic puzzles. And be sure to check out the rest of their Nrich Olympics Math as well.
Medals Count
Given the following clues, can you work out the number of gold, silver and bronze medals that France, Italy and Japan got in this international sports competition?
- Japan has 1 more gold medal, but 3 fewer silver medals, than Italy.
- France has the most bronze medals (18), but fewest gold medals (7).
- Each country has at least 6 medals of each type.
- Italy has 27 medals in total.
- Italy has 2 more bronze medals than gold medals.
- The three countries have 38 bronze medals in total.
- France has twice as many silver medals as Italy has gold medals.
Princess in the Dungeon Game
Yet more fun from Rosie at Education Unboxed. I found these while looking for videos to use in my PUFM Subtraction post. Rosie says:
This is seriously embarrassing and I debated whether to put this video online or not because this is NOT my normal personality, but my girls made up this game and will play it for over an hour and ask for it repeatedly… so I figured someone out there might be able to use it with their kids, too.
If you know me, please don’t ever ask me to do this in public. I will refuse.
Princess in the Dungeon, Part 1 – Fractions with Cuisenaire Rods





