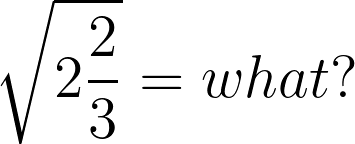This week, I’m working on graphics for my upcoming book 70+ Things to Do with a Hundred Chart. I had fun with this complex fraction image.
It looks a bit cluttered. Possible tweak: Remove the brackets and instead use a thicker dividing line to show the thirds.
While I’m thinking about that, would you like a sneak peek at an activity from the book?
Make Your Own Math
You don’t need a set of worksheets or lesson plans to learn math. All you need is an inquiring mind and something interesting to think about.
Play. Discuss. Notice. Wonder.
Enjoy.
Here’s how you can play complex fractions with your kids…
Start with Fraction Strips

Print a few blank 120 charts and turn them sideways, so each chart has ten rows with twelve squares in each row.
Cut out the rows to make fraction strips with twelve squares on each strip.
Color a different set of squares on each strip. On some strips, arrange the colored squares all together at one end. On other strips, mix them around.
If we count each strip as one whole thing, what fraction of its squares are colored?
Match the strips that represent the same fraction.
On some of the strips, there will be more than one way to name the fraction. For example, if six squares are colored, we can call that 6/12 or 2/4 or 1/2 of the strip. These alternate names are easiest to see when the colored squares are all at one end of the strip, because you can fold the strip to show the halves or fourths.
How many different fraction names can you find for each set of colored squares?
Look for Complex Fractions
We could also call the strip with six colored squares “1 1/2 thirds” of the whole strip. Can you show by folding why that name makes sense?
Or we could call the strip with five colored squares “2 1/2 sixths.”
When we have a fraction within a fraction like this, we call it a complex fraction, because it is more complicated than a common (or simple) fraction.
Another way to say it: Complex fractions have other fractions inside them.
A complex fraction is like a puzzle, challenging us to find its secret identity — the common fraction that names the same amount of stuff.
For example, how much is 3 1/3 fourths? One fourth would be three of the twelve squares on a fraction strip. So three fourths would be three sets of those three squares, or nine squares. Then we need to add one-third of the final fourth, which is one of the remaining three squares. So 3 1/3 fourths must be ten squares in all.
3 1/3 fourths = 10/12 = 5/6
How many complex fractions can you find in your set of fraction strips?
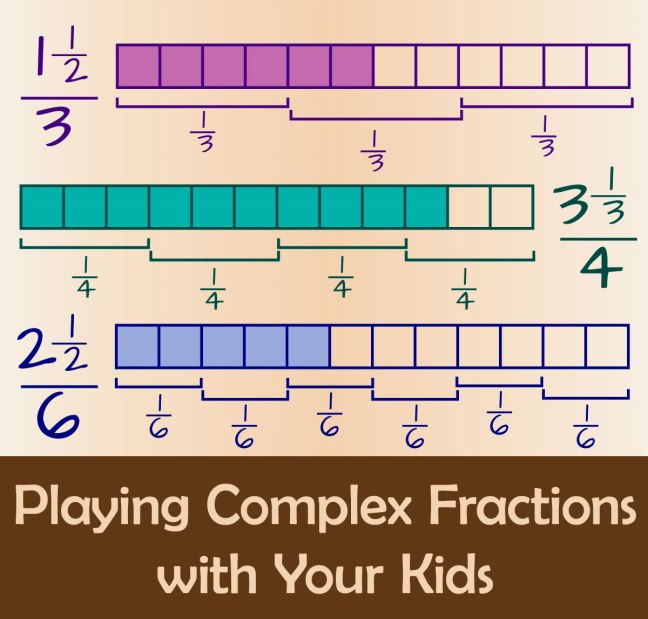
Challenge Puzzles
Can you figure out how much a one-and-a-halfth would be?
That is one piece, of such a size that it takes one and one-half pieces to make a complete fraction strip.
A one-and-a-halfth is a very useful fraction and was a favorite of the ancient Egyptian scribes, who used it to solve all sorts of practical math problems.
How about a one-and-a-thirdth? How many of those pieces make a whole strip? What common fraction names the same amount of stuff?
Or how much would a two-thirdth be? In that case, it only takes two-thirds of a piece to make a complete strip. So the whole piece must be greater than one. A two-thirdth’s secret identity is a mixed number. Can you unmask it?
Make up some challenge fraction mysteries of your own.

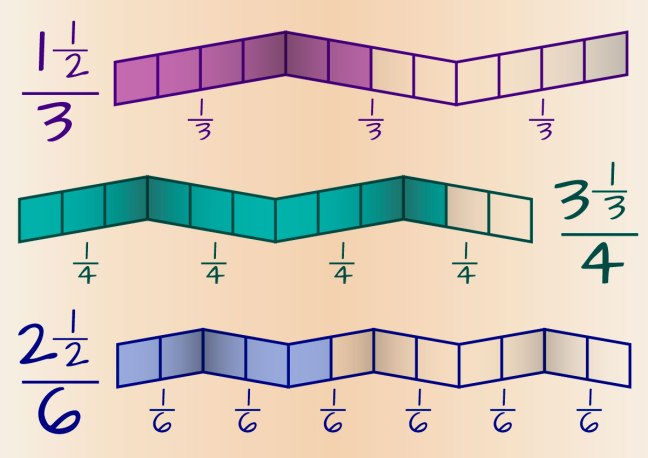
Update…
I’m still working on the graphics for my hundred chart book. Here’s the latest version of the complex fraction strips.
I like this one much better.
What do you think?

CREDITS: The slogan “Make Math Your Own” comes from Maria Droujkova, founder and director of the Natural Math website. Maria likes to say: “Make math your own, to make your own math!”
70+ Things to Do with a Hundred Chart is now available from Tabletop Academy Press.