Logic: The Centauri Challenge

Posted on by Denise Gaskins

Another fun discovery from the #MTBoS Challenge: Brian Miller (@TheMillerMath) posted this interstellar puzzle on his blog today.

centaurichallenge
[Right-click image to download a pdf you can print for your students.]

More Logic Puzzles

If you liked the Centauri Challenge, you may also enjoy the following blog posts:

Math That Is Fun: Infinite Primes

Posted on by Denise Gaskins

Oh, my! Ben Orlin over at Math with Bad Drawings just published my new favorite math proof ever:

I had a fight with Euclid on the nature of the primes.
It got a little heated – you know how the tension climbs.

It started out most civil, with a honeyed cup of tea;
we traded tales of scholars, like Descartes and Ptolemy.
But as the tea began to cool, our chatter did as well.
We’d had our fill of gossip. We sat silent for a spell.
That’s when Euclid turned to me, and said, “Hear this, my friend:
did you know the primes go on forever, with no end?” …

15-eu-must-be-clidding

Click here to read the whole post at Math with Bad Drawings.

What Is a Proof?

Posted on by Denise Gaskins

I’ve been enjoying the Introduction to Mathematical Thinking course by Keith Devlin. For the first few weeks, we mostly talked about language, especially the language of logical thinking. This week, we started working on proofs.

For a bit of fun, the professor emailed a link to this video. My daughter Kitten enjoyed it, and I hope you do, too.

Full lesson available at Ted-Ed.

Lockhart’s Measurement

Posted on by Denise Gaskins

After watching the video on the Amazon.com page, this book has jumped to the top of my wish list.

You may have read Paul Lockhart’s earlier piece, A Mathematician’s Lament, which explored the ways that traditional schooling distorts mathematics. In this book, he attempts to share the wonder and beauty of math in a way that anyone can understand.

According to the publisher: “Measurement offers a permanent solution to math phobia by introducing us to mathematics as an artful way of thinking and living. Favoring plain English and pictures over jargon and formulas, Lockhart succeeds in making complex ideas about the mathematics of shape and motion intuitive and graspable.”

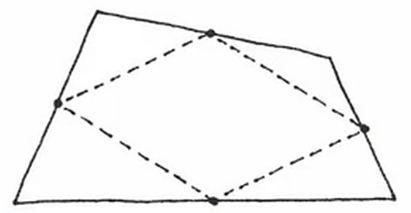
If you take any 4-sided shape at all — make it as awkward and as ridiculous as you want — if you take the middles of the sides and connect them, it always makes a parallelogram. Always! No matter what crazy, kooky thing you started with.

That’s scary to me. That’s a conspiracy.

That’s amazing!

That’s completely unexpected. I would have expected: You make some crazy blob and connect the middles, it’s gonna be another crazy blob. But it isn’t — it’s always a slanted box, beautifully parallel.

WHY is it that?!

The mathematical question is “Why?” It’s always why. And the only way we know how to answer such questions is to come up, from scratch, with these narrative arguments that explain it.

So what I want to do with this book is open up this world of mathematical reality, the creatures that we build there, the questions that we ask there, the ways in which we poke and prod (known as problems), and how we can possibly craft these elegant reason-poems.

— Paul Lockhart
author of Measurement

Sample from the Introduction to Mathematical Thinking Class

Posted on by Denise Gaskins

I’m really looking forward to Keith Devlin’s free Introduction to Mathematical Thinking class, which starts in mid-September. There are more than 30,000 nearly 40,000 students signed up already. Will you join us?

These days, mathematics books tend to be awash with symbols, but mathematical notation no more is mathematics than musical notation is music.

A page of sheet music represents a piece of music: the music itself is what you get when the notes on the page are sung or performed on a musical instrument. It is in its performance that the music comes alive and becomes part of our experience. The music exists not on the printed page but in our minds.

The same is true for mathematics. The symbols on a page are just a representation of the mathematics. When read by a competent performer (in this case, someone trained in mathematics), the symbols on the printed page come alive — the mathematics lives and breathes in the mind of the reader like some abstract symphony.

— Keith Devlin
Introduction to Mathematical Thinking

Thinking (and Teaching) like a Mathematician

Posted on by Denise Gaskins

photos by fdecomite via flickr

Most people think that mathematics means working with numbers and that being “good at math” means being able to do (only slower) what any $10 calculator can do. But then, most people think all sorts of silly things, right? That’s what makes “man on the street” interviews so funny.

Numbers are definitely part of math — but only part, and not even the biggest part. And being “good at math” means much more than being able to work with numbers. It means making connections, thinking creatively, seeing familiar things in new ways, asking “Why?” and “What if?” and “Are you sure?”

It means trying something and being willing to fail, then going back and trying something else. Even if your first try succeeded — or maybe, especially if your first try succeeded. Just knowing one way to do something is not, for a mathematician, the same as understanding that something. But the more different ways you know to figure it out, the closer you are to understanding it.

Mathematics is not just memorizing and following rules. If we want to teach real mathematics, we teachers need to learn to think like mathematicians. We need to see math as a mental game, playing with ideas. James Tanton explains:

Continue reading Thinking (and Teaching) like a Mathematician