Playful Math Carnival 144: Anniversary Edition

Posted on by Denise Gaskins

Welcome to the 144th edition of the Playful Math Education Blog Carnival — a smorgasbord of delectable tidbits of mathy fun. It’s like a free online magazine devoted to learning, teaching, and playing around with math from preschool to high school.

Bookmark this post, so you can take your time browsing.

There’s so much playful math to enjoy!

By tradition, we would start the carnival with a puzzle/activity in honor of our 144th edition. But this time, I want to take a peek back at the history of our carnival.

But if you’d rather jump straight to our featured blog posts, click here to see the Table of Contents.

Continue reading Playful Math Carnival 144: Anniversary Edition

What Is Multiplication, Anyway?

Posted on by Denise Gaskins

At some point during the process of teaching multiplication to our children, we really need to come to terms with this question:

What IS multiplication?

Did your device hide the video? Find it on YouTube here.

“What’s my answer? It’s not one that society’s going to like. Because society expects — demands, even — that mathematics be concrete, real-world, absolute, having definitive answers.

    I can’t give a definitive answer.

      Multiplication manifests itself in different ways. So maybe the word ‘is’ there is just too absolute. And it’s actually at odds with what mathematicians do.

        Mathematicians do attend to real-world, practical scenarios — by stepping away from them, looking at a bigger picture.”

        —James Tanton, What is Multiplication?

        For Further Study

        You may also enjoy these posts from my blog archive:

        Memorizing the Times Table: A Life Skills Approach

        Posted on by Denise Gaskins

        Continuing on my theme of times table facts, here’s the inimitable James Tanton:

        Did your device hide the video? Find it on YouTube here.

        “If our task is to memorize this table, please make it about mathematics — about thinking your way through a challenge, and what can I do to make my life easier.”

        —James Tanton, Making Memorising Multiplication Facts (if one really must) a meaningful Life Skill Lesson

        For Further Study

        You may also enjoy my blog post series about working through the times tables, paying attention to mathematical relationships (and a bit of prealgebra) along the way.

        Times Tables Series

        Click the button to see the whole series. Scroll down to the first post to go through it in order.

        What Are Mixed Numbers?

        Posted on by Denise Gaskins

        I just discovered a fascinating fact: In some places in the world, mixed numbers apparently don’t exist.

        So that made me curious about my blog readers:

        • Did you learn about mixed numbers in school?
        • Do you ever use mixed numbers in daily life?
        • Are your children learning to work with them?

        And if you DO know mixed numbers, can you simplify this mess:

        [If you enjoy dry math humor, the answer is worth the work.]

        Continue reading What Are Mixed Numbers?

        Exciting New Homeschool Math Program

        Posted on by Denise Gaskins

        Homeschooling friends, check out this new homeschool math program that’s fun, rigorous, and engaging — a delightful, hands-on course that helps parents (and their children) understand math.

        Introduction to Cuisenaire Rod Structures Course

        I had the privilege of previewing this class as Sonya and Lacy put it together. I highly recommend it to anyone who struggles with math, or who wants to take a non-traditional approach.

        By focusing on making sense of number relationships, and by teaching algebra before arithmetic, this course provides a stress-free path to rich mathematical mastery.

        And for all they provide, including weekly live workshops and a slew of printable math journal pages that prompt deep thinking, the price is a steal!

        Continue reading Exciting New Homeschool Math Program

        More Dover Samples

        Posted on by Denise Gaskins

        “Without mathematics you can’t do anything! Everything around you is mathematics. Everything around you is numbers.”

        —Anna Claybourne, I Can Be a Math Magician


        Dover Publications sent out a new email today with fun coloring and craft samples. And several puzzles from I Can Be a Math Magician: Fun STEM Activities for Kids by Anna Claybourne.

        Enjoy!

        If you’d like to receive future Dover Sampler emails, you can sign up here.

        THE FINE PRINT: I am an Amazon affiliate. If you follow the book link above and buy something, I’ll earn a small commission (at no cost to you).

        Free Number Sense Resources from Steve Wyborney

        Posted on by Denise Gaskins

        If you teach children in the primary grades, you’ll enjoy this new series from the wonderful Steve Wyborney. Every day for the rest of the school year, Steve will post a new estimation or number sense resource for grades K–8 (or any age!) at his blog:

        “This is my way of providing support and encouragement – as well as bringing math joy to your classroom… I’m going to stick with you all year long.”

        —Steve Wyborney

        Click to visit Steve’s blog

        Playing Math with Michael and Nash

        Posted on by Denise Gaskins

        Michael and Nash have been creating and posting new math games with astonishing regularity throughout the pandemic. Their YouTube channel is a great resource for parents who want to play math with elementary-age children.

        Today’s entry: Closest to Ten, a quick game for addition and subtraction fluency with a tiny bit of multiplication potential.

        And here’s one of my favorites for older players: Factor Triangles, a card game for 2-digit multiplication.

        Check out their channel, and have fun playing math with your kids!

        Visit Michael and Nash on YouTube

        Math for Star Wars Day

        Posted on by Denise Gaskins

        May the Fourth be with you!

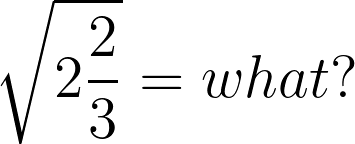
        Here is a math problem in honor of one of our family’s favorite movies…

        Han Solo was doing much-needed maintenance on the Millennium Falcon. He spent 3/5 of his money upgrading the hyperspace motivator. He spent 3/4 of the remainder to install a new blaster cannon. If he spent 450 credits altogether, how much money did he have left?

        Stop and think about how you would solve it before reading further.

        Continue reading Math for Star Wars Day