 Welcome to the 115th edition of the Playful Math Education Blog Carnival — a smorgasbord of links to bloggers all around the internet who have great ideas for learning, teaching, and playing around with math from preschool to pre-college.
Welcome to the 115th edition of the Playful Math Education Blog Carnival — a smorgasbord of links to bloggers all around the internet who have great ideas for learning, teaching, and playing around with math from preschool to pre-college.
In honor of Women’s History Month, this carnival features quotes from fifteen women mathematicians.
If you would like to jump straight to our featured blog posts, click here to see the Table of Contents.
Let the mathematical fun begin!
The Women of Mathematics
They came from many countries and followed a variety of interests.
They conquered new topics in mathematics and expanded the world’s understanding of old ones.
They wrestled with theorems, raised children, published articles, won awards, faced discrimination, led professional organizations, and kept going through both success and failure.
Some gained international renown, but most enjoyed quiet lives.
They studied, learned, and lived (and some still live) as most of us do — loving their families and friends, joking with colleagues, hoping to influence students.
I think you’ll find their words inspiring.

“What I really am is a mathematician. Rather than being remembered as the first woman this or that, I would prefer to be remembered, as a mathematician should, simply for the theorems I have proved and the problems I have solved.”
—Julia Robinson (1919–1985)

“All in all, I have found great delight and pleasure in the pursuit of mathematics. Along the way I have made great friends and worked with a number of creative and interesting people. I have been saved from boredom, dourness, and self-absorption. One cannot ask for more.”
—Karen Uhlenbeck (b. 1942)
Continue reading Playful Math Education Carnival 115—Women of Mathematics





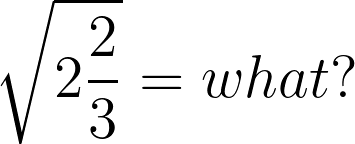

 Irish mathematician William R. Hamilton was struggling with a tough math problem in October, 1843. It had him stumped. Then on the 16th, as he walked along Dublin’s Royal Canal with his wife, inspiration struck.
Irish mathematician William R. Hamilton was struggling with a tough math problem in October, 1843. It had him stumped. Then on the 16th, as he walked along Dublin’s Royal Canal with his wife, inspiration struck. 







 Welcome to the 115th edition of the Playful Math Education Blog Carnival — a smorgasbord of links to bloggers all around the internet who have great ideas for learning, teaching, and playing around with math from preschool to pre-college.
Welcome to the 115th edition of the Playful Math Education Blog Carnival — a smorgasbord of links to bloggers all around the internet who have great ideas for learning, teaching, and playing around with math from preschool to pre-college. 
