Photo by Sister72.
Dave at MathNotations offers another version of Nim that will give your students something to think about:
[1,2]-3-[4,5]-6-[7,8]…21 Helping Children Devise and Understand Winning Strategies
Nim Revisited
Blog
Way To Go, Boys!
Photo by ccarlstead.
Congratulations, math team! All your hard work paid off, and I hope you enjoyed yourselves thoroughly. Of course, as C. S. Lewis wrote:
…if you do one good deed, your reward usually is to be set to do another and harder and better one.
Now it’s time to practice for the state level in March. You can find practice problems online at:
Preparation Drills for MATHCOUNTS
or
The “Go Figure!” math challenge
[ACK! MathCounts has re-written their website. The old link is no longer any good, but I haven’t yet found the new location for this game.]
And give the new interactive Countdown Round game a try:
500 (?) and Counting
Photo by rileyroxx.
Could this be my 500th post? That doesn’t seem possible, even counting all those half-finished-and-then-deleted drafts. Well, at least it is my 500th something, according to the WordPress.com dashboard. And surely a 500th anything is worth a small celebration, right?
Maybe my students aren’t so bad, after all…
It has been awhile since I posted a link to Rudbeckia Hirta’s Learning Curves blog. Here are a few of her students’ recent bloopers:
The Secret of Egyptian Fractions
Photo from Library of Congress via pingnews.
Archaeology professor Dr. Fibonacci Jones came home from a long day of lecturing and office work. Stepping inside the front door, he held up a shiny silver disk.
“Ta-da!” he said.
“All right!” said his daughter Alexandria. “The photos are here.”
They had to chase Alex’s brother Leon off the computer so they could view the images on the CD, but that wasn’t hard. He wanted to see the artifacts, too. Alex recognized several of the items they had dug up from the Egyptian scribe’s burial plot: the wooden palette, some clay pots, and of course the embalmed body.
Then came several close-up pictures of writing on papyrus.
Photo from MathsNet.net.
How to Write Egyptian Fractions
“I remember how to read the Egyptian numbers,” Alex said, “but what are these marks above them?”
Dr. Jones nodded. “I thought you would catch that. Those are fractions. The scribe places an open mouth, which is the hieroglyph ‘r’, over a number to make its reciprocal.”
“I know that word,” Leon said. “It means one over the number. Like, the reciprocal of 12 is 1/12, right?”
“That is right. 1/12 would be written as…”
The Rest of the Story
As I transcribed this article from my old math newsletter, I realized that it would require more graphics than I was willing to construct. LaTex does not handle Egyptian hieroglyphs — or at least, I don’t know how to make it do so. Instead, I decided to scan the newsletter pages and give them to you as a pdf file:
Right-click and choose “Save” to download:
- The secret of Egyptian fractions (pdf 364KB)
The file includes a student worksheet for Egyptian fractions from 1/2 to 9/10.
Egyptian Fractions: The Answer Sheet
The answers are now posted.
To Be Continued…
Read all the posts from the January/February 1999 issue of my Mathematical Adventures of Alexandria Jones newsletter.
January Update
Are you getting ready for the big snowstorm — or is it balmy and nice where you live? For us, the weatherman is predicting 6 to 10 inches, plus drifting. Sounds like a great night to snuggle down with pizza and a movie, assuming the power doesn’t go out.
Major Blog Changes
January was a month of major and minor changes for Let’s play math! blog. My biggest change was moving my blogroll to a separate page. This move gave me enough room to comment on several of my favorite blogs, and I hope to add more notes over the next few months.
It also freed up space in my sidebar for my new Blog parties for teachers widget. (Scroll down to see it.) I was getting frustrated posting little blurbs every time a new blog carnival came out, only to see the posts become outdated within a week — those announcements were threatening to outnumber my on-topic blog posts. Aargh! Now I can post the latest links where they are easy to find, without diluting my main-column articles.
How Should We Teach Arithmetic?
Dave Marain of MathNotations is running a poll about how to teach multiplication, but the question has broader application:
How should we teach the arithmetic algorithms
— or should we teach them at all?
Algorithms are step-by-step methods for doing something. In arithmetic, we have standard algorithms for addition, subtraction, multiplication, and long division. Once the student masters the steps for any particular algorithm, he can follow the steps to a correct answer without ever thinking about what the numbers mean.
Euclid’s Game on a Hundred Chart
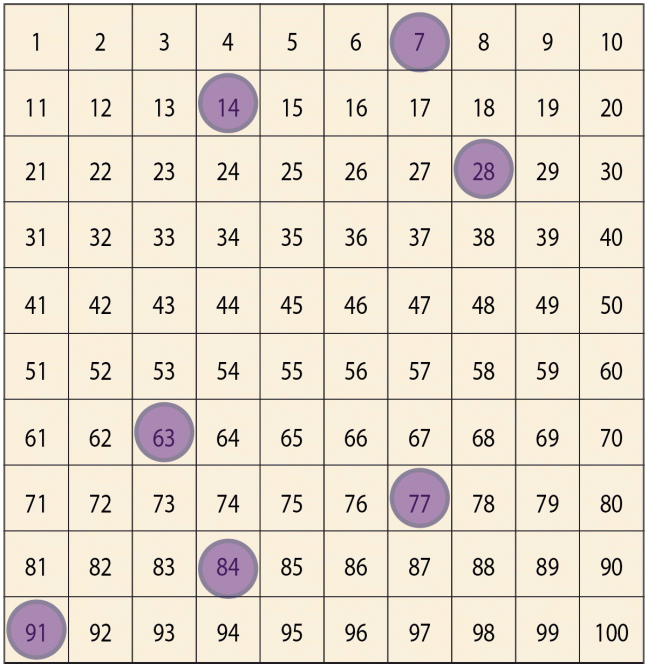
Math concepts: subtraction within 100, number patterns, mental math
Number of players: 2 or 3
Equipment: printed hundred chart (also called a hundred board), and highlighter or translucent disks to mark numbers — or use this online hundred chart
Set Up
Place the hundred chart and highlighter where all players can reach them.
How to Play
- Allow the youngest player choice of moving first or second; in future games, allow the loser of the last game to choose.
- The first player chooses a number from 1 to 100 and marks that square on the hundred chart.
- The second player chooses and marks any other number.
- On each succeeding turn, the player subtracts any two marked numbers to find and mark a difference that has not yet been taken.
- Play alternates until no more numbers can be marked.
Quotations XIX: How Do We Learn Math?
He doesn’t learn algebra
in the algebra course;
he learns it in calculus.
I have been catching up on my Bloglines reading [procrastinating blogger at work — I should be going over the MathCounts lesson for Friday’s homeschool co-op class], and found the following quotation at Mathematics under the Microscope [old blog posts are no longer archived].
That’s Mathematics
Things are still hectic, but at least the phone company guy found the problem and got our “extended DSL” service working. “Extended DSL” is what you get when you live out in the boonies. No guarantees that it will be faster than the ancient modem, but at least it doesn’t tie up the phone line anymore.
And it is a bit faster, so I finally get to enjoy You Tube. If the video doesn’t display properly, you can find it at this link:
The Game of Algebra
My pre-algebra class hit the topic of equations just as the NFL season moved into the playoffs. The result was this series of class notes called “The Game of Algebra.”
We used the Singapore Math NEM 1 textbook, which is full of example problems and quality exercises. These notes simply introduce or review the main concepts and vocabulary in a less-textbooky way.
I hope you find them useful.
Denise Gaskins' Let's Play Math 